Propeller torque & engine torque
Join Date: Oct 2009
Location: UK
Posts: 1,270
Likes: 0
Received 0 Likes
on
0 Posts
Hi Keith,
Thanks for your lucid explanations. Would you please point out where my logic is failing here.
Ignoring form drag for simplicity:
Consider an aircraft performing continuous rate 1 turns holding over a beacon flying at a speed of V. The wing develops lift and consequently induced drag ID.
Therefore, induced drag power = ID*V.
For sustained flight the thrust power from the propeller must match the induced drag power, therefore THP = ID*V
Consider the model aircraft in a vertical hover. The propeller is now a rotary wing. It is producing lift in a similar way to the aircraft wing, by moving through the air with some velocity Vp and consequently generating induced drag IDp.
The power required to spin the rotary wing (the propeller in this case) = IDp*Vp.
They look very similar to me.
Thanks for your lucid explanations. Would you please point out where my logic is failing here.
Ignoring form drag for simplicity:
Consider an aircraft performing continuous rate 1 turns holding over a beacon flying at a speed of V. The wing develops lift and consequently induced drag ID.
Therefore, induced drag power = ID*V.
For sustained flight the thrust power from the propeller must match the induced drag power, therefore THP = ID*V
Consider the model aircraft in a vertical hover. The propeller is now a rotary wing. It is producing lift in a similar way to the aircraft wing, by moving through the air with some velocity Vp and consequently generating induced drag IDp.
The power required to spin the rotary wing (the propeller in this case) = IDp*Vp.
They look very similar to me.
Happy to oblige.
In the paragraph above you are using the thrust multiplied by the AICRAFT VELOCITY to get the THP. That is entirely correct
In this second paragraph the thing that you are calling a "rotary wing" is really just a helicopter rotor or else a propeller. You are then taking the drag that it produces (in the plane of rotation), and multiplying it by the rotational velocity.
That's OK as long as you realise that what you have worked out is the power that is required to keep your prop turning. But this is BHP.
If you want to calculate THP for your rotary wing aircraft you need to multiply the THRUST IN THE DIRETION OF FLIGHT by the AIRCRAFT VELOCITY not by the ROTOR VELOCITY. Neither the thrust nor the aircraft velocity have been included in your description of the schenario.
I don't know if you have studied rotary wing pof very much, but if you look at the power available/power required curves you will find that they are very different from the fixed wing cuves. There is a thing that is called induced power. It is the power that is required to induce the airflow down through the main rotor. Induced power varies markedly with forward speed and it takes into account the varying rotor efficiency (including such things as the tilt of the rotors in forward flight). Because this varying efficiency is taken into account in the induced power curve, the power available curve is shown as a straight(ish) line. This line is really the BHP/SHP. I suspect that you will find few if any references to THP in rotary wing POF.
A number of contributions to this thread have included attempts to draw comparisons between rotary wing pof and fixed wing pof. This is unlikely to be very helpful because the two are very different in many ways. The fact is that few of us know enough about rotary wing pof to make the comparisons very illuminating (I certainly don't)
I have invited oggers to go back to basics and explain why he thinks that an aeroplane that is not moving (brakes on or hovering model) is generating THP. I think that this exercise will be more productive than thinking up imaginary scenarious about circling aircraft and rotating wings. You might like to try it.
Ignoring form drag for simplicity:
Consider an aircraft performing continuous rate 1 turns holding over a beacon flying at a speed of V. The wing develops lift and consequently induced drag ID.
Therefore, induced drag power = ID*V.
For sustained flight the thrust power from the propeller must match the induced drag power, therefore THP = ID*V
Consider an aircraft performing continuous rate 1 turns holding over a beacon flying at a speed of V. The wing develops lift and consequently induced drag ID.
Therefore, induced drag power = ID*V.
For sustained flight the thrust power from the propeller must match the induced drag power, therefore THP = ID*V
Consider the model aircraft in a vertical hover. The propeller is now a rotary wing. It is producing lift in a similar way to the aircraft wing, by moving through the air with some velocity Vp and consequently generating induced drag IDp.
The power required to spin the rotary wing (the propeller in this case) = IDp*Vp.
The power required to spin the rotary wing (the propeller in this case) = IDp*Vp.
That's OK as long as you realise that what you have worked out is the power that is required to keep your prop turning. But this is BHP.
If you want to calculate THP for your rotary wing aircraft you need to multiply the THRUST IN THE DIRETION OF FLIGHT by the AIRCRAFT VELOCITY not by the ROTOR VELOCITY. Neither the thrust nor the aircraft velocity have been included in your description of the schenario.
I don't know if you have studied rotary wing pof very much, but if you look at the power available/power required curves you will find that they are very different from the fixed wing cuves. There is a thing that is called induced power. It is the power that is required to induce the airflow down through the main rotor. Induced power varies markedly with forward speed and it takes into account the varying rotor efficiency (including such things as the tilt of the rotors in forward flight). Because this varying efficiency is taken into account in the induced power curve, the power available curve is shown as a straight(ish) line. This line is really the BHP/SHP. I suspect that you will find few if any references to THP in rotary wing POF.
A number of contributions to this thread have included attempts to draw comparisons between rotary wing pof and fixed wing pof. This is unlikely to be very helpful because the two are very different in many ways. The fact is that few of us know enough about rotary wing pof to make the comparisons very illuminating (I certainly don't)
I have invited oggers to go back to basics and explain why he thinks that an aeroplane that is not moving (brakes on or hovering model) is generating THP. I think that this exercise will be more productive than thinking up imaginary scenarious about circling aircraft and rotating wings. You might like to try it.
Last edited by keith williams; 13th Apr 2012 at 23:06.
Join Date: Feb 2005
Location: flyover country USA
Age: 82
Posts: 4,579
Likes: 0
Received 0 Likes
on
0 Posts
oggers:
Exactly, because it's a different kind of efficiency - i.e. a measure of how much STATIC thrust can be had, compared to some theoretical "perfect" static thrust. That's altogether different from propulsive efficiency, which is
= 100% x (Thrust horsepower) / (engine output hp)
In other words, efficiency = output / input !
But, he is careful to point out that it cannot be used to determine the efficiency of a prop in the static thrust situation. It is - according to him - "invalid" in that situation. So, he uses a different equation for that.
= 100% x (Thrust horsepower) / (engine output hp)
In other words, efficiency = output / input !
We can calculate the efficiency of any process that we choose to look at.
How efficiently do I digest my food? (not very efficiently, judging by how much I eat and how little exercise I do)
How efficiently do my children use my money? (not at all efficiently)
How efficiently does the government use my taxes (worse than my kids)
If you want to look at how efficiently a propeller produces thrust then that's OK, but it is not propeller efficiency.
Propeller efficiency = THP / BHP
THP and BHP both have very specific definitions, which means that propeller efficiency also has a very specific definition.
THP = Thrust x Aircraft Velocity
So Propeller efficiency = Thrust x Aircraft velocity / BHP
So you will not prove that a propeller is producing THP when the aircraft is not moving.
I (and most of the people reading this thread) am happy to accept the fact that when an aircraft is being held on the brakes, the propeller does a lot of work in propelling the propwash rearwards. But it is doing no work whatsoever in propelling the aeroplane forwards. So it is producing no THP.
As I said to oggers in a pervious post:
How efficiently do I digest my food? (not very efficiently, judging by how much I eat and how little exercise I do)
How efficiently do my children use my money? (not at all efficiently)
How efficiently does the government use my taxes (worse than my kids)
If you want to look at how efficiently a propeller produces thrust then that's OK, but it is not propeller efficiency.
Propeller efficiency = THP / BHP
THP and BHP both have very specific definitions, which means that propeller efficiency also has a very specific definition.
THP = Thrust x Aircraft Velocity
So Propeller efficiency = Thrust x Aircraft velocity / BHP
So you will not prove that a propeller is producing THP when the aircraft is not moving.
I (and most of the people reading this thread) am happy to accept the fact that when an aircraft is being held on the brakes, the propeller does a lot of work in propelling the propwash rearwards. But it is doing no work whatsoever in propelling the aeroplane forwards. So it is producing no THP.
As I said to oggers in a pervious post:
If we look again at the basics:
Work is done when a force moves its point of application in the direction of the force.
Work = force x distance.
Power is the rate of doing work
Power = Force x distance / time
Power = force x velocity
From the above we can see that THP = Thrust x aircraft velocity.
Now look at your hovering model aeroplane and give us a logical explanation of why you believe that some THP is being produced.
Work is done when a force moves its point of application in the direction of the force.
Work = force x distance.
Power is the rate of doing work
Power = Force x distance / time
Power = force x velocity
From the above we can see that THP = Thrust x aircraft velocity.
Now look at your hovering model aeroplane and give us a logical explanation of why you believe that some THP is being produced.
Join Date: Feb 2000
Location: Alaska, PNG, etc.
Age: 60
Posts: 1,550
Likes: 0
Received 0 Likes
on
0 Posts
Originally Posted by Aerobat77
one more thing , but maybe i understand you not right : the 19600 in/lbs must be the value for the torque on the propeller, not the turbine by itself since a device which spins 13800rpm and produces simultany massive 19600 in/lb of torque would have an asronomic power ( 19600x13800/5252 = 51500 shp!!! )
Join Date: Feb 2005
Location: flyover country USA
Age: 82
Posts: 4,579
Likes: 0
Received 0 Likes
on
0 Posts
A Squared:
Very good breakdown of the SHP problem. I've been stung by that "factor of 12" issue before - it's egg-on-your-face big time!
I will, however, point out 1 or 2 little items: Torque units are properly called "pound-feet" (or "pound-inches") and not "foot-pounds"; the foot-pound is a unit of energy or work.
And the constant 5252 is easy to remember, but it happens to be the quotient of 33000/6.2832 (or 2 pi). I once derived this on my own, many decades ago when I still had sufficient active neurons.
Very good breakdown of the SHP problem. I've been stung by that "factor of 12" issue before - it's egg-on-your-face big time!
I will, however, point out 1 or 2 little items: Torque units are properly called "pound-feet" (or "pound-inches") and not "foot-pounds"; the foot-pound is a unit of energy or work.
And the constant 5252 is easy to remember, but it happens to be the quotient of 33000/6.2832 (or 2 pi). I once derived this on my own, many decades ago when I still had sufficient active neurons.

Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
Keith Williams and barit1:
You say THP is thrust x velocity. I agree. But I say that only works for a specific set of assumptions. Static thrust is not the only scenario that doesn’t conform to the assumptions. Here is another:
Aircraft flying straight and level at speed Va, pilot sets new power to accelerate to Vb. Assume constant propeller efficiency between Va and Vb due variable prop. Final THP = thrust x Vb, we agree that much. Using the hypothesis you outlined above we can draw some conclusions:
The new power is set, the BHP has gone to the prop but THP doesn’t catch up until the plane reaches Vb?!
Thrust horsepower during the acceleration is less than final THP when you get to Vb?!
Thrust must have increased, but this didn’t reflect an increase in THP, this was because power was wasted in the propwash?!
It’s all a bit odd, if that’s what you believe. Personally I simply accept that the increase in power results in an increase in THP in accordance with the equation THP = BHP x PE. And that work done on the propwash isn’t wasted if it’s giving thrust.
You say there are two types of power output from the prop. The two types you identify are “wasted propwash power” and “THP”. You both favour this over the common aircraft performance terminology which considers power available to be simply: ‘THP’.
To be clear, nobody is saying that no power is lost in the propwash otherwise THP would simply equal BHP. But that is different from what you are implying – that all the work done on the air is a waste and only work done on the aircraft counts toward THP:
According to Hubert C Smith, Associate Professor Emeritus, Penn State, in his “Illustrated Guide to Aerodynamics”:
“actual power available for thrust is obtained by multiplying BHP times propeller efficiency”
“The [amount of power] available is the thp, which is the bhp times propeller efficiency”
… the same equation you both keep ignoring that appears in numerous sources including the USN training doc already referenced in this thread:
THP = BHP x Propeller Efficiency
…and this quote from the same USN reference: “Thrust horsepower (THP) is propeller output, or the power that is converted to usable thrust by the propeller. The ability of the propeller to turn engine output into thrust is given by its propeller efficiency (p.e.).”
…which directly contradicts the position you both hold:
In fact, you have both made it clear that you believe a prop with zero propeller efficiency can still produce thrust! And please don’t repeat the equation for propulsive efficiency because it is not valid unless you observe the assumption it depends upon; namely, equilibrium flight. Therefore I have to say the assertions you are making are not credible opinions to hold, but such is the level of cognitive dissonance required to believe in this meme of zero THP for a hovering aircraft. Let’s see it again:
...zero propeller efficiency, zero thrust horsepower, and zero useful work on propwash. I don't think so.
“When the aircraft is stationary on the ground with engine running all of the propeller power output is being wasted in accelerating the propwash rearwards. So none of the propeller power output is being delivered to the airframe. That means that there is no THP, because as Barit has said "THP is the power delivered to the airframe".
In theory if the aircraft were to fly at its own propwash speed no power would be wasted in the propwash, so all of the propeller power output would be being delivered to the airframe. So it would all be THP. This is of course only true in theory because if the aircraft was flying at its own propwash speed, no air would be being accelerated rearwards by the propeller, so there would be no thrust.
At any speed between the zero and the propwash speed some of the propeller power output would be being wasted in the propwash and the rest would be being delivered to the airframe as THP.
If you think about it this means that the propeller power output is the THP plus the power wasted in the propwash. So we cannot say that propeller power output is THP.
BUT. If you look at any fixed wing diagram of power available against power required you would see that the power available is the THP. It would perhaps be better to say that this is the USEFUL power available.
Beacuse THP is the power being delivered to the airframe, it is thrust x aircraft speed.”
In theory if the aircraft were to fly at its own propwash speed no power would be wasted in the propwash, so all of the propeller power output would be being delivered to the airframe. So it would all be THP. This is of course only true in theory because if the aircraft was flying at its own propwash speed, no air would be being accelerated rearwards by the propeller, so there would be no thrust.
At any speed between the zero and the propwash speed some of the propeller power output would be being wasted in the propwash and the rest would be being delivered to the airframe as THP.
If you think about it this means that the propeller power output is the THP plus the power wasted in the propwash. So we cannot say that propeller power output is THP.
BUT. If you look at any fixed wing diagram of power available against power required you would see that the power available is the THP. It would perhaps be better to say that this is the USEFUL power available.
Beacuse THP is the power being delivered to the airframe, it is thrust x aircraft speed.”
You say THP is thrust x velocity. I agree. But I say that only works for a specific set of assumptions. Static thrust is not the only scenario that doesn’t conform to the assumptions. Here is another:
Aircraft flying straight and level at speed Va, pilot sets new power to accelerate to Vb. Assume constant propeller efficiency between Va and Vb due variable prop. Final THP = thrust x Vb, we agree that much. Using the hypothesis you outlined above we can draw some conclusions:
The new power is set, the BHP has gone to the prop but THP doesn’t catch up until the plane reaches Vb?!
Thrust horsepower during the acceleration is less than final THP when you get to Vb?!
Thrust must have increased, but this didn’t reflect an increase in THP, this was because power was wasted in the propwash?!
It’s all a bit odd, if that’s what you believe. Personally I simply accept that the increase in power results in an increase in THP in accordance with the equation THP = BHP x PE. And that work done on the propwash isn’t wasted if it’s giving thrust.
You say there are two types of power output from the prop. The two types you identify are “wasted propwash power” and “THP”. You both favour this over the common aircraft performance terminology which considers power available to be simply: ‘THP’.
To be clear, nobody is saying that no power is lost in the propwash otherwise THP would simply equal BHP. But that is different from what you are implying – that all the work done on the air is a waste and only work done on the aircraft counts toward THP:
If you think about it this means that the propeller power output is the THP plus the power wasted in the propwash. So we cannot say that propeller power output is THP. BUT. If you look at any fixed wing diagram of power available against power required you would see that the power available is the THP. It would perhaps be better to say that this is the USEFUL power available.
“actual power available for thrust is obtained by multiplying BHP times propeller efficiency”
“The [amount of power] available is the thp, which is the bhp times propeller efficiency”
… the same equation you both keep ignoring that appears in numerous sources including the USN training doc already referenced in this thread:
THP = BHP x Propeller Efficiency
…and this quote from the same USN reference: “Thrust horsepower (THP) is propeller output, or the power that is converted to usable thrust by the propeller. The ability of the propeller to turn engine output into thrust is given by its propeller efficiency (p.e.).”
…which directly contradicts the position you both hold:
“you think that if thrust is not zero then propeller efficiency cannot be zero. If you do believe this, then you are wrong (once again).”
...zero propeller efficiency, zero thrust horsepower, and zero useful work on propwash. I don't think so.
Join Date: Feb 2000
Location: Alaska, PNG, etc.
Age: 60
Posts: 1,550
Likes: 0
Received 0 Likes
on
0 Posts
Originally Posted by barit1
A Squared:
Very good breakdown of the SHP problem. I've been stung by that "factor of 12" issue before - it's egg-on-your-face big time!
Very good breakdown of the SHP problem. I've been stung by that "factor of 12" issue before - it's egg-on-your-face big time!
Originally Posted by barit1
I will, however, point out 1 or 2 little items: Torque units are properly called "pound-feet" (or "pound-inches") and not "foot-pounds"; the foot-pound is a unit of energy or work.
I can't recall ever being confused about whether I was talking about torque, or work and energy
As far as "pound-inches" I have to say, I haven't ever heard that one. I do know that the torque meters on my Herc (and all the official literature associated with it) uses "inch-pounds".
Oggers,
It's a bit too late for me to reply to your post tonight.
For the moment, would you please state what you believe to be the correct equation for propeller efficiency.
It's a bit too late for me to reply to your post tonight.
For the moment, would you please state what you believe to be the correct equation for propeller efficiency.
Join Date: Feb 2005
Location: flyover country USA
Age: 82
Posts: 4,579
Likes: 0
Received 0 Likes
on
0 Posts
oggers, please re-read post #144. I made it pretty clear that there are two kinds of efficiency, one for static thrust, and one for propulsive efficiency. Please - when you refer to "efficiency" - make it clear which you are talking about.
Smith here is referring to propulsive efficiency - where the plane is being propelled. Don't use this for the stationary example.
According to Hubert C Smith, Associate Professor Emeritus, Penn State, in his “Illustrated Guide to Aerodynamics”:
“actual power available for thrust is obtained by multiplying BHP times propeller efficiency”
“The [amount of power] available is the thp, which is the bhp times propeller efficiency”
“actual power available for thrust is obtained by multiplying BHP times propeller efficiency”
“The [amount of power] available is the thp, which is the bhp times propeller efficiency”
You say THP is thrust x velocity. I agree. But I say that only works for a specific set of assumptions. Static thrust is not the only scenario that doesn’t conform to the assumptions. Here is another:
Aircraft flying straight and level at speed Va, pilot sets new power to accelerate to Vb. Assume constant propeller efficiency between Va and Vb due variable prop. Final THP = thrust x Vb, we agree that much. Using the hypothesis you outlined above we can draw some conclusions:
The new power is set, the BHP has gone to the prop but THP doesn’t catch up until the plane reaches Vb?!
Thrust horsepower during the acceleration is less than final THP when you get to Vb?!
Thrust must have increased, but this didn’t reflect an increase in THP, this was because power was wasted in the propwash?!
Aircraft flying straight and level at speed Va, pilot sets new power to accelerate to Vb. Assume constant propeller efficiency between Va and Vb due variable prop. Final THP = thrust x Vb, we agree that much. Using the hypothesis you outlined above we can draw some conclusions:
The new power is set, the BHP has gone to the prop but THP doesn’t catch up until the plane reaches Vb?!
Thrust horsepower during the acceleration is less than final THP when you get to Vb?!
Thrust must have increased, but this didn’t reflect an increase in THP, this was because power was wasted in the propwash?!
OK lets’ look at your scenario and see if it really proves your point.
To simplify the situation and to avoid any ambiguities we will assume the following:
1. The aircraft is initially in steady non-accelerated flight. This means that the power required is equal to the THP being generated.
2. The initial speed Va is greater than Vmd so any increase in speed will produce an increase in drag and an increase in power required.
3. There is no reduction gearbox between the engine and the propeller, so the full engine torque is applied to the propeller.
4. The propeller is of the constant speed –variable pitch type.
5. To increase the power, the pilot simply pushes the throttle forward (selecting a higher RPM would just complicate the argument, but not really change the outcome).
6. The pilot has decided to increases airspeed simply by increasing the engine power output (you have already intimated this, but it is best to avoid unnecessary arguments about how best to increase airspeed).
With the aircraft in steady flight at constant RPM the engine torque (causing the propeller to rotate) will be equal and opposite of the propeller torque (the component of propeller total reaction that acts in the plane of rotation to oppose rotation in powered flight). This balance of two opposing torques will maintain a constant propeller RPM.
When the pilot opens the throttle the power output (BHP) of the engine will increase. The increased power will initially take the form of an increase in engine torque. This will cause engine torque to become greater than propeller torque, so the propeller RPM will start to increase.
When the propeller constant speed unit senses this increase in RPM, it will command the pitch change unit to increase the pitch of the propeller blades. This will increase the angle of attack of the blades, thereby increasing propeller total reaction. This in turn will increase both the propeller torque and the thrust. The increased propeller torque will cause the RPM to return to its initial (selected) value. So the overall effects of the pilot opening the throttle will be an increase in thrust, which will cause an immediate increase in THP.
Prior to the pilot opening the throttle, the aircraft was in steady balanced flight, so the thrust was equal to the drag and the power required (drag x TAS) was equal to the THP (thrust x TAS).
The increased thrust caused by the pilot opening the throttle would have the following effects:
1. The thrust would be greater than the drag.
2. The THP being generated would be greater than the power required.
The combination of thrust greater than drag and THP greater than power required would cause the airspeed to increase. As the airspeed increases, it would cause the drag and hence the power required to increase. The acceleration would continue until the increasing drag was once again equal to the thrust and the increasing power required was equal to the THP being generated. The aircraft would then settle at the new into balanced flight at the new higher speed.
Now let’s look again at your comments:
The new power is set, the BHP has gone to the prop but THP doesn’t catch up until the plane reaches Vb?!
Thrust horsepower during the acceleration is less than final THP when you get to Vb?!
Thrust horsepower during the acceleration is less than final THP when you get to Vb?!
Static thrust is not the only scenario that doesn’t conform to the assumptions. Here is another:
work done on the propwash isn’t wasted if it’s giving thrust.
As an aircraft flies through the air it is continuously losing energy due to the drag force. If the airspeed and altitude are to be maintained, this lost energy must be replenished at a rate that is equal to the loss rate. Looked at in this context the purpose of the propulsion system is to take energy from the fuel, convert it into kinetic energy and transfer it to the aircraft. Any energy that is lost to the propwash (or jet efflux) represents a waste of energy.
The enormous improvements in fuel efficiency that have been achieved in turbojets / turbofans over the past few decades have been brought about by reducing the amount of kinetic energy that is wasted in the jet efflux. The old turbojets were quite able to produce thrust, but their very high exhaust velocities meant that they were throwing away enormous amounts of kinetic energy. The fact that modern engines are able produce the same (or even more) thrust, while throwing away much less energy, shows that the energy loss is wasteful.
I am quite happy to respond to the remainder of your post when you have stated the equation that you consider to be correct for propeller efficiency.
Join Date: Oct 2009
Location: UK
Posts: 1,270
Likes: 0
Received 0 Likes
on
0 Posts
Propeller Efficiency
Hi oggers,
Have a look at:Propeller Aircraft Performance and The Bootstrap Approach: Background
"Of the four forces acting on the airplane – thrust, drag, lift, and weight – thrust is the most difficult to measure or predict. That is why most books about aircraft performance simply assume that propeller efficiency h is some constant. Commonly cited values are h = 80% and h = 85%. Then thrust T = h P, where P is the engine power. Unfortunately, propeller efficiency is in fact not constant; it varies with air speed and RPM or, more precisely, with the dimensionless ratio of those two variables:
J=V/nd
where J is the "propeller advance ratio." As the propeller rotates through one circle the airplane advances a distance V/n. J is then the ratio of that advance distance to the propeller’s diameter.
Figure 1 is an example of how propeller efficiency varies with advance ratio."
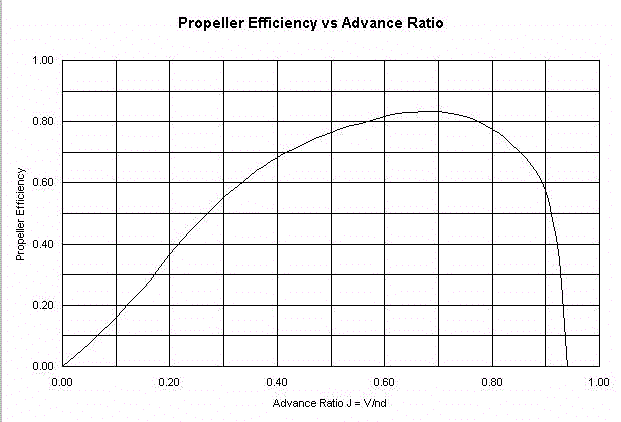
If there is zero advance, then efficiency = 0
Have a look at:Propeller Aircraft Performance and The Bootstrap Approach: Background
"Of the four forces acting on the airplane – thrust, drag, lift, and weight – thrust is the most difficult to measure or predict. That is why most books about aircraft performance simply assume that propeller efficiency h is some constant. Commonly cited values are h = 80% and h = 85%. Then thrust T = h P, where P is the engine power. Unfortunately, propeller efficiency is in fact not constant; it varies with air speed and RPM or, more precisely, with the dimensionless ratio of those two variables:
J=V/nd
where J is the "propeller advance ratio." As the propeller rotates through one circle the airplane advances a distance V/n. J is then the ratio of that advance distance to the propeller’s diameter.
Figure 1 is an example of how propeller efficiency varies with advance ratio."

If there is zero advance, then efficiency = 0
Rudderrudderrat,
If Oggers had wanted to accept the fact that propeller efficiency is zero when forward speed is zero, he just needed to read the Essay to which he referred on page 4 of this thread.
It includes a graph that is pretty much like yours, but it shows propeller efficiency against forward speed.
And it starts at zero-zero!


If Oggers had wanted to accept the fact that propeller efficiency is zero when forward speed is zero, he just needed to read the Essay to which he referred on page 4 of this thread.
It includes a graph that is pretty much like yours, but it shows propeller efficiency against forward speed.
And it starts at zero-zero!



Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
keith Williams:
.
<<Thrust Horsepower: The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill Dictionary of Aviation
Zero thrust horsepower ≡ zero thrust. The model requires thrust to hover therefore the THP is not zero.
Power is required for thrust additional to losses. It is the induced power of the prop/rotor. In the case of the model ‘prop hanging’, that induced power is the thrust times the velocity induced at the prop, along the thrust axis. Induced power is therefore equivalent to thrust horsepower.
The position you are sticking to is that all power going into the slipstream is wasted power, which is true in the context of aircraft velocity but not in the context of thrust. Hence, propulsive efficiency for velocity, and FOM for thrust:
“Since it is the induced power which relates to the useful function of the rotor, the ratio of induced power to total power is a measure of rotor efficiency in the hover. This ratio is called the Figure of Merit” Sedddon: Basic Helicopter Aerodynamics
For a given prop the thrust depends on both induced velocity Vi and the mass flow through the prop: T = ρA(Va + Vi) x ΔV. Va may go to zero but if Vi goes to zero you have no thrust. Statically, the “power converted to thrust” is T x Vi. You will find this is in accordance with simple momentum theory for a prop as well as the definition at the top. It is therefore THP.
Non-statically this is T x (Va + Vi) which eventually becomes ≈ T x Va only. You have said as much but the point that T x Va is actually an approximation (though it is definitive for propulsive power) of ‘power converted to thrust’ seems to have escaped you. In the latter case it is fair to say that THP = T Va and swallow the approximation. But this becomes invalid at low speed as I have been stressing all along. This graph shows where the approximation holds good as the curves run along the top near 100% beginning at about 20m/s for lightly loaded props:
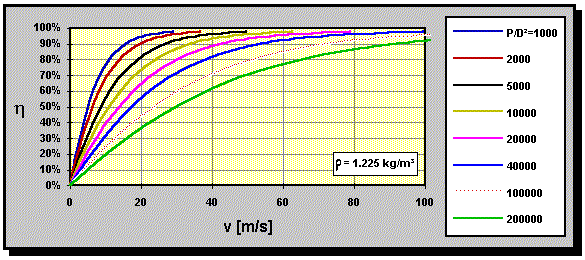
The efficiency increases as mass flow through the prop picks up at speed.
The graph in the essay is the same as the one above. These are Froude efficiency curves. It does not show that THP goes to zero with Va for a given BHP which is what you think. The speedier end of the curve shows Froude efficiency ≈ 100% of induced efficiency whereas the slower end of the curve shows the opposite. Ergo TVa is a good proxy for induced power at one end of the curve but completely invalid at the other end.
When you add BET you get a graph like the one RRT posted for overall propulsive efficiency. Personally, when I compare the two graphs I see they are “pretty much alike” in the same way that r is pretty much like n (ie different). The r shaped curve is showing that Froude efficiency increases as a proportion of overall efficiency and stays there even after overall efficiency drops off again so TVa as a proportion of “power converted to thrust” stays high. OTOH, as speed goes down the approximation fails. That is the whole point of the essay, the very reason the guy felt the need:
"you should see a problem in that as your velocity goes to zero, no matter how much thrust you're producing, your efficiency goes to zero. So how do you know how good your prop is doing at low speeds or statically?"
..and he spends most of the essay working around the problem.
Looking at the model again, the position that you and barit1 have adopted is that the model has zero THP whilst prop hanging but some THP if it climbs. Therefore it has negative THP if it descends and the prop will drive the engine. In that case you are in autorotation as soon as you start to descend (or shortly after when -THP is sufficient to offset profile power). That would be nice, but it’s not the case. Autorotation does not begin until after RoD exceeds Vi. Any helicopter pilot will tell you that auto requires a healthy rate of descent, not merely a slight descent.
By contrast, if you take THP = induced power = T (Va + Vi) then you have THP in the hover, more THP in the climb and less THP in the descent until RoD exceeds Vi and autorotation begins. You will find this is in agreement with momentum theory for a helicopter in descent.
I find the comparison to be very helpful because as far as momentum theory goes the rotor and the prop are precisely the same. And we don’t need to go beyond that to determine the induced power required to provide a given thrust.
Well, here are 3 credible definitions of THP:
<<The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill dictionary of aviation
<<THP: The horsepower equivalent of the thrust produced by a turbojet or turbofan engine>> FAA Handbook of Aeronautical Knowledge.
<<The amount of power that gets converted into thrust is referred to as thrust horsepower or thp>> Hubert C Smith Ph.D. Associate Professor Emeritus, Penn State
There is absolutely no doubt that the model is developing induced power T x (Va + Vi). That is a given. Induced power is the power converted to thrust for the model or lift for the helicopter. It fits all three of those definitions, whereas T x Va is an approximation that only works when the Froude efficiency is high. Ergo it is invalid statically.
I have invited oggers to go back to basics and explain why he thinks that an aeroplane that is not moving (brakes on or hovering model) is generating THP. I think that this exercise will be more productive than thinking up imaginary scenarious about circling aircraft and rotating wings. You might like to try it
<<Thrust Horsepower: The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill Dictionary of Aviation
Zero thrust horsepower ≡ zero thrust. The model requires thrust to hover therefore the THP is not zero.
Power is required for thrust additional to losses. It is the induced power of the prop/rotor. In the case of the model ‘prop hanging’, that induced power is the thrust times the velocity induced at the prop, along the thrust axis. Induced power is therefore equivalent to thrust horsepower.
The position you are sticking to is that all power going into the slipstream is wasted power, which is true in the context of aircraft velocity but not in the context of thrust. Hence, propulsive efficiency for velocity, and FOM for thrust:
“Since it is the induced power which relates to the useful function of the rotor, the ratio of induced power to total power is a measure of rotor efficiency in the hover. This ratio is called the Figure of Merit” Sedddon: Basic Helicopter Aerodynamics
For a given prop the thrust depends on both induced velocity Vi and the mass flow through the prop: T = ρA(Va + Vi) x ΔV. Va may go to zero but if Vi goes to zero you have no thrust. Statically, the “power converted to thrust” is T x Vi. You will find this is in accordance with simple momentum theory for a prop as well as the definition at the top. It is therefore THP.
Non-statically this is T x (Va + Vi) which eventually becomes ≈ T x Va only. You have said as much but the point that T x Va is actually an approximation (though it is definitive for propulsive power) of ‘power converted to thrust’ seems to have escaped you. In the latter case it is fair to say that THP = T Va and swallow the approximation. But this becomes invalid at low speed as I have been stressing all along. This graph shows where the approximation holds good as the curves run along the top near 100% beginning at about 20m/s for lightly loaded props:

The efficiency increases as mass flow through the prop picks up at speed.
If Oggers had wanted to accept the fact that propeller efficiency is zero when forward speed is zero, he just needed to read the Essay to which he referred on page 4 of this thread. It includes a graph that is pretty much like yours, but it shows propeller efficiency against forward speed. And it starts at zero-zero! 





When you add BET you get a graph like the one RRT posted for overall propulsive efficiency. Personally, when I compare the two graphs I see they are “pretty much alike” in the same way that r is pretty much like n (ie different). The r shaped curve is showing that Froude efficiency increases as a proportion of overall efficiency and stays there even after overall efficiency drops off again so TVa as a proportion of “power converted to thrust” stays high. OTOH, as speed goes down the approximation fails. That is the whole point of the essay, the very reason the guy felt the need:
"you should see a problem in that as your velocity goes to zero, no matter how much thrust you're producing, your efficiency goes to zero. So how do you know how good your prop is doing at low speeds or statically?"
..and he spends most of the essay working around the problem.
Looking at the model again, the position that you and barit1 have adopted is that the model has zero THP whilst prop hanging but some THP if it climbs. Therefore it has negative THP if it descends and the prop will drive the engine. In that case you are in autorotation as soon as you start to descend (or shortly after when -THP is sufficient to offset profile power). That would be nice, but it’s not the case. Autorotation does not begin until after RoD exceeds Vi. Any helicopter pilot will tell you that auto requires a healthy rate of descent, not merely a slight descent.
By contrast, if you take THP = induced power = T (Va + Vi) then you have THP in the hover, more THP in the climb and less THP in the descent until RoD exceeds Vi and autorotation begins. You will find this is in agreement with momentum theory for a helicopter in descent.
“A number of contributions to this thread have included attempts to draw comparisons between rotary wing pof and fixed wing pof. This is unlikely to be very helpful because the two are very different in many ways. The fact is that few of us know enough about rotary wing pof to make the comparisons very illuminating (I certainly don't)”
THP and BHP both have very specific definitions, which means that propeller efficiency also has a very specific definition.
THP = Thrust x Aircraft Velocity
THP = Thrust x Aircraft Velocity
Well, here are 3 credible definitions of THP:
<<The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill dictionary of aviation
<<THP: The horsepower equivalent of the thrust produced by a turbojet or turbofan engine>> FAA Handbook of Aeronautical Knowledge.
<<The amount of power that gets converted into thrust is referred to as thrust horsepower or thp>> Hubert C Smith Ph.D. Associate Professor Emeritus, Penn State
There is absolutely no doubt that the model is developing induced power T x (Va + Vi). That is a given. Induced power is the power converted to thrust for the model or lift for the helicopter. It fits all three of those definitions, whereas T x Va is an approximation that only works when the Froude efficiency is high. Ergo it is invalid statically.
Join Date: Aug 1999
Location: England
Posts: 1,050
Likes: 0
Received 0 Likes
on
0 Posts
Well, here are 3 credible definitions of THP:
<<The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill dictionary of aviation
<<THP: The horsepower equivalent of the thrust produced by a turbojet or turbofan engine>> FAA Handbook of Aeronautical Knowledge.
<<The amount of power that gets converted into thrust is referred to as thrust horsepower or thp>> Hubert C Smith Ph.D. Associate Professor Emeritus, Penn State
<<The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill dictionary of aviation
<<THP: The horsepower equivalent of the thrust produced by a turbojet or turbofan engine>> FAA Handbook of Aeronautical Knowledge.
<<The amount of power that gets converted into thrust is referred to as thrust horsepower or thp>> Hubert C Smith Ph.D. Associate Professor Emeritus, Penn State
really, none of those definitions is any more precise than saying 'well, its kind of like this.....'
I bet if you asked Hubert C Smith to give you a formula relating THP and thrust he would say: THP = Thrust x TAS.
pb
The author of the essay to which you have repeatedly referred did not actually state that the equation is invalid as speed approaches zero. What he actually said was:
While working on a project designing a propeller at work, I wanted to know just how good I was doing. Efficiency is one measure of how well a propeller is performing, but it's not necessarily a good indication of how well the design is performing up to its potential. In aviation, propulsive efficiency is defined as:
Efficiency = T x V / Pavail
where η is efficiency, T is Thrust, V is Velocity, and Pavail is Power Available, or power going into the propeller. Basically, power out divided by power in. This equation is very useful for many cases, but you should see a problem in that as your velocity goes to zero, no matter how much thrust you're producing, your efficiency goes to zero.
The author of the essay had a problem because he was attempting to use the propeller efficiency equation to calculate thrust. He was assuming that the purpose of the propeller is to produce thrust, but this is not true.
The purpose of the propeller is to propel the aircraft forward against the drag force, by producing thrust. The rate at which the propeller is achieving this purpose is equal to the thrust multiplied by the aircraft velocity. This is our old friend the THP.
Because the primary purpose of the propeller is to propel the aircraft forward, it is entirely logical that the overall efficiency of the propeller should be measured in terms of its propulsive efficiency.
Propeller efficiency = (Thrust x Aircraft Velocity/ Brake Horsepower
This can also be stated as (Thrust x TAS) / BHP provided we take care to note that the TAS is velocity of the aircraft relative to the air and is not the propwash velocity.
When the aircraft is running at full throttle on the ground, with the wheel brakes preventing it from moving forward, the propeller is absorbing power but is not achieving any success in propelling the aircraft forward. So the propeller efficiency is zero, which is exactly what the equation yields. The equation is in fact producing the correct result at all airspeeds including zero.
To understand why the author of the essay could not use the equation to calculate thrust when airspeed was zero we need to look at what he was attempting to do.
He was attempting to take the product of (Thrust x zero airspeed) and then divide it by zero airspeed to reveal the thrust.
For any number other than zero and infinity this would be a perfectly reasonable thing to do.
But the product of any number multiplied by zero is zero, and dividing this product by zero simply gives zero / zero = zero.
The simple fact is that the processes of multiplication and division are not reversible when one of the numbers is zero. This fact is not a function of any inaccuracies in the propeller efficiency equation. It is simply the result of one of the properties of the number zero. Any equation involving multiplication and division will encounter exactly the same problem when one of the values goes to zero. But this does not mean that all such equations are invalid.
Entering autorotation in a helicopter is not simply a matter of throttling back the power until the aircraft starts to descend. If you do this, the blades will stall, the rotor speed will decrease, the blades will fold upwards and the aircraft to crash. To enter autorotation you must lower the collective to get negative pitch (or at least a very low pitch) at which the ROD airflow produces an angle of attack, such that part of the total reaction drives the blades forward. This keeps the rotors turning and keeps generating lift. None of these good things will happen if we simply reduce power in a propeller driven aircraft, because the mechanisms are physically very different. Your use of this scenario simply illustrates your lack of knowledge regarding helicopter POF.
<<The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill dictionary of aviation
<<THP: The horsepower equivalent of the thrust produced by a turbojet or turbofan engine>> FAA Handbook of Aeronautical Knowledge.
<<The amount of power that gets converted into thrust is referred to as thrust horsepower or thp>> Hubert C Smith Ph.D. Associate Professor Emeritus, Penn State
In the second of your definitions the term “horsepower equivalent of the thrust” implies that it is the thrust x TAS. So this definition is quite correct.
In dealing with your first and third definitions I could quite easily find numerous sources of the definition THP = Thrust x TAS. I have at least one example on my office bookshelf. But trading references will prove nothing. Instead let’s see what your definitions produce in terms of a propeller efficiency equation.
Efficiency is simply a ratio of output divided by input, and standard efficiency equations are of the form Efficiency = Output / Input
In your first and third definitions the output is thrust and the input is power.
So we have Efficiency = Thrust output / Power input
If we use imperial units of pounds force for thrust and foot pounds force per minute for power we get:
Efficiency = (lbf) / (ft lbf / min)
Cancelling out the lbf on the top and bottom of this equation we get
Efficiency = 1 / ft/min which is Efficiency = min/ft.
The equation has yielded an efficiency figure that is in units of minutes per foot. What exactly does this mean?
Efficiency is just a ratio of output divided by input, so it has no units.
To get rid of the min/ft in our result we need to multiply by ft/min. But ft/mins are the units of velocity, so to get a proper value for efficiency we need to multiply by velocity. This converts our efficiency equation into Efficiency = (Thrust x TAS) / Power input.
This is of course the propulsive efficiency equation.
The above sequence proves something that we should already have known. That is the fact that power, which is the rate of doing work or expending energy, cannot be converted into a force. Power and force are two totally different things and one cannot be converted into another. So whatever the sources of your first and second definitions, they cannot be correct. It is of course possible that the authors did not intend their definitions to be interpreted literally.
Finally I think that you need to look again at your argument that induced power is the same things at THP. I have drawn the following quotes from various internet sources.
Induced power is the power required to maintain enough lift to overcome the force of gravity.
www.math.usu.edu/~powell/ornlab-html/node7.html
Induced Power is that portion of the power required to produce lift.
www.griffin-helicopters.co.uk/note/helicopterpower.htm - 13k
The minimum engine power required to hover is called the "induced power."
scienceworld.wolfram.com/physics/Helicopter.html - 15k
Induced power is what people are referring to when they say helicopters "beat the air into submission." Newton's 2nd law concerning action-reaction applies in this regime where we must force air down to keep the aircraft aloft.
www.navair.navy.mil/safety/documents/Power_Available_vs.doc
In each case they show that induced power is exclusively concerned with the process of generating lift. THP is concerned with propelling aircraft through the air, so they are not the same thing. By all means argue that your model aeroplane is generating induced power. But it is most certainly not generating any THP.
While working on a project designing a propeller at work, I wanted to know just how good I was doing. Efficiency is one measure of how well a propeller is performing, but it's not necessarily a good indication of how well the design is performing up to its potential. In aviation, propulsive efficiency is defined as:
Efficiency = T x V / Pavail
where η is efficiency, T is Thrust, V is Velocity, and Pavail is Power Available, or power going into the propeller. Basically, power out divided by power in. This equation is very useful for many cases, but you should see a problem in that as your velocity goes to zero, no matter how much thrust you're producing, your efficiency goes to zero.
The author of the essay had a problem because he was attempting to use the propeller efficiency equation to calculate thrust. He was assuming that the purpose of the propeller is to produce thrust, but this is not true.
The purpose of the propeller is to propel the aircraft forward against the drag force, by producing thrust. The rate at which the propeller is achieving this purpose is equal to the thrust multiplied by the aircraft velocity. This is our old friend the THP.
Because the primary purpose of the propeller is to propel the aircraft forward, it is entirely logical that the overall efficiency of the propeller should be measured in terms of its propulsive efficiency.
Propeller efficiency = (Thrust x Aircraft Velocity/ Brake Horsepower
This can also be stated as (Thrust x TAS) / BHP provided we take care to note that the TAS is velocity of the aircraft relative to the air and is not the propwash velocity.
When the aircraft is running at full throttle on the ground, with the wheel brakes preventing it from moving forward, the propeller is absorbing power but is not achieving any success in propelling the aircraft forward. So the propeller efficiency is zero, which is exactly what the equation yields. The equation is in fact producing the correct result at all airspeeds including zero.
To understand why the author of the essay could not use the equation to calculate thrust when airspeed was zero we need to look at what he was attempting to do.
He was attempting to take the product of (Thrust x zero airspeed) and then divide it by zero airspeed to reveal the thrust.
For any number other than zero and infinity this would be a perfectly reasonable thing to do.
But the product of any number multiplied by zero is zero, and dividing this product by zero simply gives zero / zero = zero.
The simple fact is that the processes of multiplication and division are not reversible when one of the numbers is zero. This fact is not a function of any inaccuracies in the propeller efficiency equation. It is simply the result of one of the properties of the number zero. Any equation involving multiplication and division will encounter exactly the same problem when one of the values goes to zero. But this does not mean that all such equations are invalid.
Looking at the model again, the position that you and barit1 have adopted is that the model has zero THP whilst prop hanging but some THP if it climbs. Therefore it has negative THP if it descends and the prop will drive the engine. In that case you are in autorotation as soon as you start to descend (or shortly after when -THP is sufficient to offset profile power). That would be nice, but it’s not the case. Autorotation does not begin until after RoD exceeds Vi. Any helicopter pilot will tell you that auto requires a healthy rate of descent, not merely a slight descent.
Entering autorotation in a helicopter is not simply a matter of throttling back the power until the aircraft starts to descend. If you do this, the blades will stall, the rotor speed will decrease, the blades will fold upwards and the aircraft to crash. To enter autorotation you must lower the collective to get negative pitch (or at least a very low pitch) at which the ROD airflow produces an angle of attack, such that part of the total reaction drives the blades forward. This keeps the rotors turning and keeps generating lift. None of these good things will happen if we simply reduce power in a propeller driven aircraft, because the mechanisms are physically very different. Your use of this scenario simply illustrates your lack of knowledge regarding helicopter POF.
Well, here are 3 credible definitions of THP:
<<The amount of horsepower the engine-propeller combination transforms into thrust.>> McGraw-Hill dictionary of aviation
<<THP: The horsepower equivalent of the thrust produced by a turbojet or turbofan engine>> FAA Handbook of Aeronautical Knowledge.
<<The amount of power that gets converted into thrust is referred to as thrust horsepower or thp>> Hubert C Smith Ph.D. Associate Professor Emeritus, Penn State
In the second of your definitions the term “horsepower equivalent of the thrust” implies that it is the thrust x TAS. So this definition is quite correct.
In dealing with your first and third definitions I could quite easily find numerous sources of the definition THP = Thrust x TAS. I have at least one example on my office bookshelf. But trading references will prove nothing. Instead let’s see what your definitions produce in terms of a propeller efficiency equation.
Efficiency is simply a ratio of output divided by input, and standard efficiency equations are of the form Efficiency = Output / Input
In your first and third definitions the output is thrust and the input is power.
So we have Efficiency = Thrust output / Power input
If we use imperial units of pounds force for thrust and foot pounds force per minute for power we get:
Efficiency = (lbf) / (ft lbf / min)
Cancelling out the lbf on the top and bottom of this equation we get
Efficiency = 1 / ft/min which is Efficiency = min/ft.
The equation has yielded an efficiency figure that is in units of minutes per foot. What exactly does this mean?
Efficiency is just a ratio of output divided by input, so it has no units.
To get rid of the min/ft in our result we need to multiply by ft/min. But ft/mins are the units of velocity, so to get a proper value for efficiency we need to multiply by velocity. This converts our efficiency equation into Efficiency = (Thrust x TAS) / Power input.
This is of course the propulsive efficiency equation.
The above sequence proves something that we should already have known. That is the fact that power, which is the rate of doing work or expending energy, cannot be converted into a force. Power and force are two totally different things and one cannot be converted into another. So whatever the sources of your first and second definitions, they cannot be correct. It is of course possible that the authors did not intend their definitions to be interpreted literally.
Finally I think that you need to look again at your argument that induced power is the same things at THP. I have drawn the following quotes from various internet sources.
Induced power is the power required to maintain enough lift to overcome the force of gravity.
www.math.usu.edu/~powell/ornlab-html/node7.html
Induced Power is that portion of the power required to produce lift.
www.griffin-helicopters.co.uk/note/helicopterpower.htm - 13k
The minimum engine power required to hover is called the "induced power."
scienceworld.wolfram.com/physics/Helicopter.html - 15k
Induced power is what people are referring to when they say helicopters "beat the air into submission." Newton's 2nd law concerning action-reaction applies in this regime where we must force air down to keep the aircraft aloft.
www.navair.navy.mil/safety/documents/Power_Available_vs.doc
In each case they show that induced power is exclusively concerned with the process of generating lift. THP is concerned with propelling aircraft through the air, so they are not the same thing. By all means argue that your model aeroplane is generating induced power. But it is most certainly not generating any THP.
Join Date: Feb 2005
Location: flyover country USA
Age: 82
Posts: 4,579
Likes: 0
Received 0 Likes
on
0 Posts
keith williams:
Well done! 
...The author of the essay had a problem because he was attempting to use the propeller efficiency equation to calculate thrust. He was assuming that the purpose of the propeller is to produce thrust, but this is not true.
The purpose of the propeller is to propel the aircraft forward against the drag force, by producing thrust. The rate at which the propeller is achieving this purpose is equal to the thrust multiplied by the aircraft velocity. This is our old friend the THP.
The purpose of the propeller is to propel the aircraft forward against the drag force, by producing thrust. The rate at which the propeller is achieving this purpose is equal to the thrust multiplied by the aircraft velocity. This is our old friend the THP.

Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
Entering autorotation in a helicopter is not simply a matter of throttling back the power until the aircraft starts to descend. If you do this, the blades will stall, the rotor speed will decrease, the blades will fold upwards and the aircraft to crash. To enter autorotation you must lower the collective to get negative pitch (or at least a very low pitch) at which the ROD airflow produces an angle of attack, such that part of the total reaction drives the blades forward. This keeps the rotors turning and keeps generating lift. None of these good things will happen if we simply reduce power in a propeller driven aircraft, because the mechanisms are physically very different. Your use of this scenario simply illustrates your lack of knowledge regarding helicopter POF.
 What I wrote was that your description of what constitutes THP implies you would be in auto as soon as Thrust x RoD (equivalent to T x TAS) exceeded profile power, when what actually happens is that auto begins when RoD exceeds induced velocity by enough to offset profile power. This is a fact.
What I wrote was that your description of what constitutes THP implies you would be in auto as soon as Thrust x RoD (equivalent to T x TAS) exceeded profile power, when what actually happens is that auto begins when RoD exceeds induced velocity by enough to offset profile power. This is a fact.
the mechanisms are physically very different
when what actually happens is that auto begins when RoD exceeds induced velocity by enough to offset profile power.
So even with a helicopter, the autorotative force does not become significant until a certain ROD has been achieved. But none of this confirms your argument that induced power is the same thing as THP
The actual mechanical arrangement is superfluous, this is about the over-arching physics. Simple momentum theory considers only that a 'disc' accelerates air. This does not tell you if the model is mechanically capable of going into auto, it tells you the theoretical relationship between induced velocity, RoD and thrust.
Any helicopter pilot will tell you that auto requires a healthy rate of descent, not merely a slight descent.
Throughout this thread you have made various assertions, including the following:
1. Propellers continue produce THP when the aircraft velocity is zero.
2. When an aeroplane is standing still on the ground with wheel brakes applied the THP is equal to Thrust x propwash velocity.
3. If propellers produced no THP when the aeroplane is standing still on the ground, it will be impossible for the aeroplane to accelerate when the brakes are released.
4. If THP is Thrust x TAS it will be impossible for aircraft to accelerate in flight.
5. THP is the same thing as Induced Power.
6. The propulsive efficiency equation is not the correct equation for propeller efficiency (though interestingly you have never actually stated what the correct equation is).
7. As long as a propeller is producing thrust its efficiency cannot be zero.
In each case your assertions have been incorrect. You have certainly demonstrated tenacity in pursuing these arguments for so long, but you have also demonstrated a very poor understanding of these subjects.
Last edited by keith williams; 21st Jun 2012 at 15:40.





