TAS from RAS, Altitude and Temperature.

[JDCAVE]

For the record, I am not a pilot although I do have a quantitative background. However, I am researching my father F/Lt Cave, 419 Squadron WWII. I have thousands of pages of wartime documents, that relate directly to his service, his service files, log books photos. I have essays on all of his 31 operations during the period 27-September-1944 to 25-March-1945. One particularly interesting operation was to Chemnitz, 5/6-March-1945. I have the navigator's log (Form 441) and chart completed for this operation by dad's navigator, F/O Seale, as well as 3 others. It would be an understatement to say these are fascinating documents which detail, minute by minute the flight of the aircraft that night.

The first page of the Form 441, includes the meteorological forecast, the flight plan with turning points and speeds. The flight plan includes a row for each turning point, Latitude, Longitude RAS, Ground Speed, Wind Speed, Wind direction, Height and outside air temperature. The navigator has calculated "Required Track True", which he adjusts using wind speed and direction and TAS, to calculate "Course True" which is then adjusted for "VARN" or Magnetic Declination. He then calculates Distance to Run between Turning Points from the Latitudes and Longitudes. Next, he calculates ground speed from TAS, Required Track True, Course True, and wind speed and direction. Note: I have verified all of these calculations, including headings and great circle distances, from simple trigonometry. Differences between my calculations and those by my father's navigator are very small and likely due to rounding or very small mechanical error as a result of the Mark III D Navigation Computer, in use at that time.

However...I am struggling with the calculation of TAS. I cannot come up with a historical formula (from 80 years ago) on calculating this parameter. Virtually everything I can find on the web is difficult to interpret in this situation. F/O Seale uses RAS (what I understand to be "Rectified Air Speed". This parameter is provided to aircrew from the "Operational Orders" (AKA Form "Bs") which they term "Indicated Air Speed" i.e. visible to the pilot on his Air Speed Indicator calibrated in MPH (yes, MPH--I know this to be true). So Seale must have used Indicated Airspeed, recorded as RAS (Rectified Air Speed) together with height and forecast air temperature to calculate TAS.

From a post (1) entitled “TAS from IAS, PA and OAT” from this forum (I am not allowed to post the URL) came up on a search and post #8 is compelling as he comments "Was given to me long time ago by an old retired navigator and it's surprisingly accurate." However, I cannot get this formula to match the results, which I will post in the next post.

Jim

(1) this one ? TAS from IAS, PA and OAT - PPRuNe Forums

JT

[CHAPARRAL]

See https://pilotworkshop.com/tips/pilot_true_airspeed/.
On the old days we used the E-6B…
Cheers!

[eckhard]

A good rule of thumb to find the difference between RAS and TAS is approx 1.5% of TAS per 1000ft of altitude (assuming ISA temp).

For example, assuming a TAS of 250MPH, the difference between TAS and RAS at 15,000 would be

15 x 1.5% of 250 =
15 x 3.75 =
56MPH

So the RAS would be approx 250 - 56 = 194MPH

The big problem with this method is that you need to guess the TAS to start with, whereas the RAS is right in front of you! A bit of iteration is required.

[JDCAVE]

Here is the information for the Calculation of TAS in F/O Seale's Log:
Column 1: R.A.S.
Column 2: Seale Height
Column 3: Seale Temp
Column 4: Seale TAS (Mph)
Column 5: Cave TAS (Calculated by Multivariate regression model: (TAS-RAS)/RAS = 0.02375 Height + 0.5985 (ln Temperature in degrees Kelvin) - 3.41581, Adjusted R2: 0.9963

170 8500 -8 192 191
170 8500 -8 192 191
170 8500 -8 192 191
170 8500 -8 192 191
170 8500 -8 192 191
170 8500 -8 192 191
158 13000 -20 190 190
160 15500 -26 200 200
160 15500 -26 200 200
165 15500 -26 206 206
165 15500 -26 206 206
165 15500 -26 206 206
180 15500 -26 225 225
195 15000 -25 242 242
200 8000 -11 222 221
195 5500 -6 208 207
180 9000 -9 204 204
200 5000 -2 214 211
180 2500 4 182 182
180 2500 4 182 182
180 2500 4 182 182
180 2500 4 182 182
180 2500 4 182 182

The Multivariate model comes very close to Seale's calculations, except for the record emphasized in bold. If someone has an E6B calculator, perhaps they could looked at this outlier. I want to point out my use of "ln Temperature in Degrees Kelvin" is because the relationship between Temperature and Height is clearly non-linear and you cannot take a log transform of a negative number, hence degrees Kelvin. The problem I have is I am using a regression model with Seale's data and results to back calculate Seale's results. It is a "circular" process and not statistically valid.

Thanks in advance for any help. Note I am still not allowed to post a photo, so you will have to wait to see a screen capture of Seales Log.

Jim

[john_tullamarine]

Back in the day, military folks used whichever nav computer to run the sums (either Dalton for the Allies or Knemeyer for the Axis). As a sidenote, the massive penetration into the market of these two basically blew all the others out of the water. The Knemeyer, for whatever reason, subsequently fell into disuse (why is totally beyond me as it was a pretty neat bit of kit) although Lahr's computer (subsequently the Jepp CR) can trace its lineage back to Knemeyer's device.

The TAS calculation is/was simple and just used the air density (from altitude and OAT) to correct EAS (which you can dumb down to CAS or IAS with minor errors - one just needs to keep in mind that CAS gets to be a bit average once the mach number ventures much above about 0.25 - the reason the techo folks invented EAS)

A typical link is Airspeed Conversions (CAS/EAS/TAS/Mach) | AeroToolbox

The equation is the usual TAS = EAS / (1/√σ) where σ is the density ratio ρ/ρo (apologies, I can't find a convenient way to make the o a subscript). When setting pressure height and OAT in the relevant box (or the density height in the adjacent box), all the device is doing is acting as a look-up table and setting the sigma factor on the outer C/D slide rule scale in preparation for the above multiplication in the usual slide rule way of doing things. Easy peasy.

However, running a multivariate regression is neither necessary nor useful for understanding.

The various rules of thumb calculations one sees are really not necessary when the slide rule (nav computer) calculation is quite a straightforward exercise.

If my recollections be correct, RAS is/was the Brit term for CAS.

PS I've located the thread Jim refers to and linked to it in his first post.

Jim, if you like to email me the scan, I can put it into your post on your behalf.

[JDCAVE]

Thanks John.

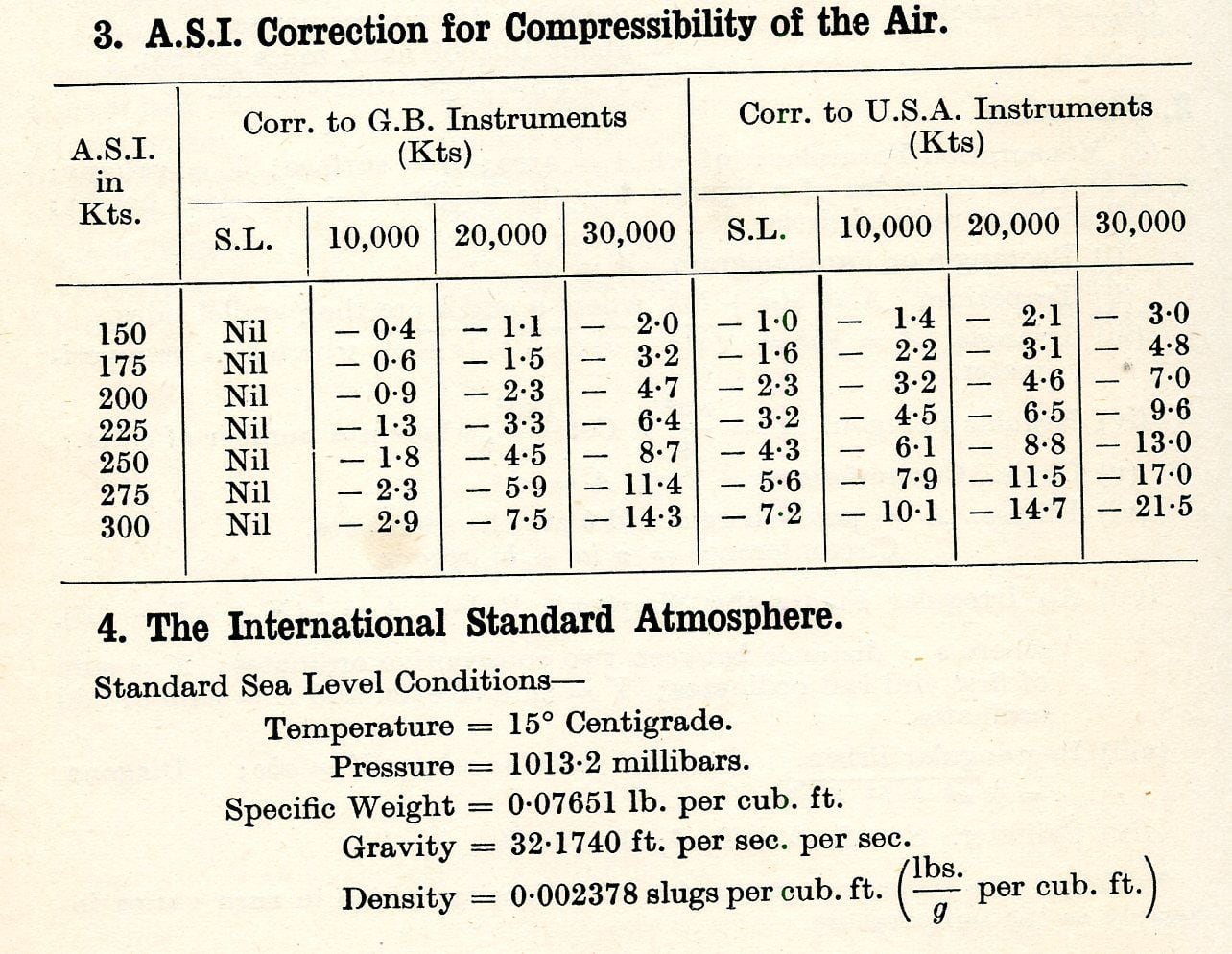
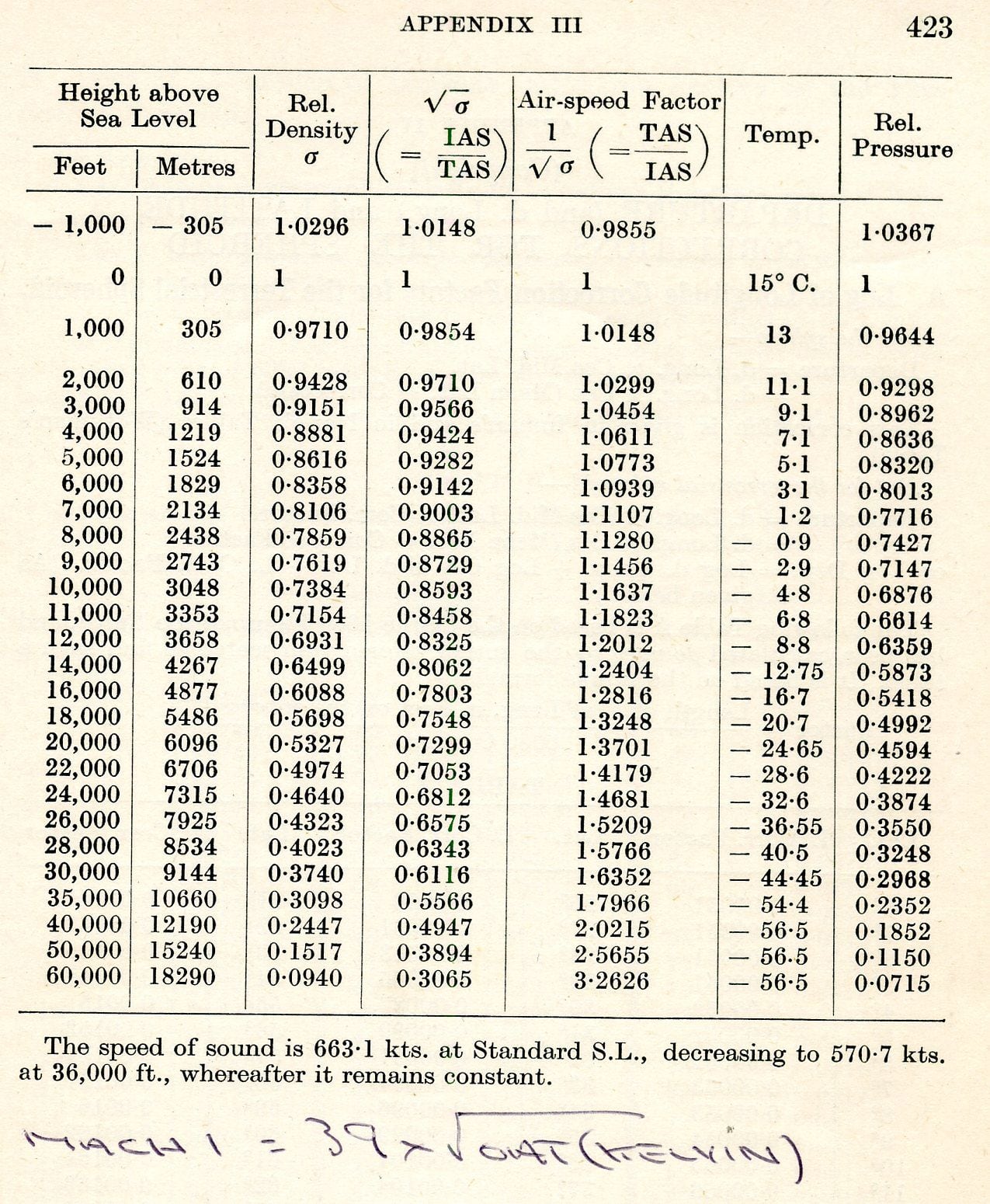
You said "The equation is the usual TAS = EAS / (1/√σ) where σ is the density ratio ρ/ρo..." Yes. I understand. That's where I am at. I have the relevant pages in DCT Bennett's book "The Complete Air Navigator" This book was in my father's library. I would post these but when I tried just now, I lost my post. I think there is enough in the section on the calculation of TAS from IAS (page 170), together with Appendix IV (4.) on The International Standard Atmosphere, which has columns for 1/√σ and √σ, Temperature and Relative Pressure at height..

Jim

[mustafagander]

What I've been using in the bug smashers for decades is TAS increases by 2% per 1,000ft over IAS. It's more than good enough given the accuracy of your instrumentation in the average bug smasher. For me it just works.

[eckhard]

I like that better than my rule of thumb! You’re starting with IAS instead of guessing the TAS.

[JDCAVE]

Thanks for the responses. I am sure that simpler calculations and “rules of thumb” are appropriate in many/most situations, however I require the exact formulae “imbedded” in the navigator’s Mark III D Navigation Computer, in use at that time, in order for me to reproduce the navigator’s calculations with accuracy. Second, after 4 hours of flying time navigators were expected to have that aircraft over the Target +/- 2 minutes of their allotted time: navigators were reprimanded for greater deviations. On the trip to Bochum 9-October-1944, dad was 6.5 minutes early and dad’s navigator was reprimanded in that case. In a telephone conversation I had with him some 4 years ago, prior to their next trip Seale said the Navigation Leader took him aside and told him “Anymore screw-ups like that Seale and you will be in serious trouble.” These times were critical in keeping the Bomber Stream concentrated along the route and over the target area, to keep the defences overwhelmed and the bombing matched up with the pathfinder’s target marking. But I digress…

I have attached two key pages from DCT Bennett’s book “The Complete Air Navigator.” I think these provide the info I need to get to Seale’s result. Bennett provides the detail on adjustments for Temperature: “…if temperature differs from the standard for the height, (see appendix IV 4), then the “pressure height” (corrected altitude with index reading from 1013.2 mbs) must be converted to “density height” by subtracting about 118.8’ for each degree above standard temperature, and vice versa.” This is key as all corrections are in height in feet and can be converted into a robust formula. Of course AVM DCT Bennett was the AOC of 8-Group Pathfinders.

Let’s see if I am allowed to attach some images…nope! I’m not.

Jim

[Commander Taco]

Jim,
Fascinating stuff. A book based on the nitty-gritty of flying an op would be terrific. Keep it coming!

[megan]

These the pages you need from Bennett?

[john_tullamarine]

Ah, slugs/cubic foot - real numbers !

However, the computer calculation does it straight from the equation for density via the sigma variable. One just plugs in the values in the wheel and the wheel does a simple look up via equation to get the sigma factor. This it puts on the outer C/D scale which sets up the multiplication ... easy peasy.

[Alex Whittingham]

The compressibility correction is different depending on whether the instruments are GB or USA? Does anyone have any further info on this concept, please?

[john_tullamarine]

The compressibility correction is different

This is a new one for me, also. My take -

(a) the early instrument makers were not able to model the full equations into an analogue device (and, yet, Huber did that in his computer in the late 40s - go figure ?)

(b) the outcome was that they had to take a shortcut. My understanding has always been that this was to restrict the ASI to standard SL conditions.

(c) my speculation is that the folk on opposite sides of the pond developed slightly different analogue models which would account for differences in calibration as suggested in Bennett's document ?

Perhaps, sometime when I have a (very) slow day, I might play with the equations and see if I can come up with the numeric deltas in the document.


Once again it never ceases to amaze me at the incredibly interesting stuff which comes out of the woodwork in PPRuNe. And, yet again, my good colleague, Megan, demonstrates his quite incredible ability to find obscure stuff in the said woodwork ... well done, once again, good sir.

[Alex Whittingham]

Could be... follow on questions would be (1) When did they stop requiring different corrections? and (2) did they then change the Daltons or their equivalent? This might explain slightly different outputs on various nav computers. The Dalton has always given slightly different results to the plastic CRP-5 loved by the UK CAA examiners.

[MrBernoulli]

Originally Posted by Alex Whittingham

This might explain slightly different outputs on various nav computers. The Dalton has always given slightly different results to the plastic CRP-5 loved by the UK CAA examiners.

It is thought provoking, Alex.

Prior to undertaking all the CAA ATPL examinations I wrote to the CAA, asking whether the use of my fathers Aristo Aviat 617 (German-manufactured, late 1960s/very early 1970's vintage?) flight-planning computer would be acceptable for the CAA exam. The CAA confirmed, in writing, that it would be.

I had already discovered that some results on the Aviat differed slightly from the RAF's 'Computer Dead Reckoning Mk 4A', but I thought I would probably manage. However, I eventually decided to fork out the dosh for a CRP-5, because it was just much easier to be talking the same language as the other prospective ATPL-ers, using the CRP-5, on your course at Bristol airport (in the portacabins, around 2002 or 2003!). 😉

[JDCAVE]

Thanks Megan! I have my volume of DTC Bennett's the Compete Air Navigator to a good friend, and had to ask him to photograph the relevant pages. I did not receive page 144. Also see page 170 which is Appendix IV (4).

I have completed my work and now have some formulae:

Course True (AKA True Heading)=RQDTrack+DEGREES(ASIN(WindS/TAS*SIN(RADIANS(RQDTrack-WindD+180))))
Ground Speed=(TAS*COS(RADIANS(RQD Track-Course True)))+(WindS*COS(RADIANS(RQD Track-WindD+180)))

Here's the tricky one, TAS:

'TAS=ROUND((1+(((118.8*(TEMP-(HEIGHT*-0.001983+15.014))+HEIGHT)/1000)^2*0.00025351+((118.8*(TEMP-(HEIGHT*-0.001983+15.014))+HEIGHT)/1000)*0.01333941+0.00364865))*RAS,0)

The relationship between RAS and TAS with correction in Height with Temperature is a polynomial, R-Squared is 0.9999. The polynomial is definitely the best fit of 1/√σ at height. So Height is corrected for the deviation of OAT from Standard Temperature at Height.

With this formula, I get quite close to Seale's calculation with a "Mean Absolute Percent Error" (MAPE) of 0.64%. The comparison of the Ground Speed (G/S) calculations (Seale's and Mine) gives a MAPE of 1%, so close.

I find that my calculation of TAS is biased at very low heights (<3,000'). The fit of the polynomial model does not handle this well. The problem is the fit of 1/√σ at height is non-linear and Bennett provides no clue as to how this should be fitted. Remember, non-linear fitting would be severely challenged in the late 1930's when his book was published.

Remember, I am not a pilot. Only an enthusiastic amateur historian with a quantitative itch!

Note: I am still unable to post photos or other attachments. I get an error message that I am unable to post a URL, even though my message has no URL. I think the attachment of my calculation would be informative.

Jim

[JDCAVE]

Here is a PDF of my calculations:

Note: I have just received a "new" to me publication, AIR NAVIGATION, Volume 1, Air Ministry 1944. This should be interesting to review.

Jim

[JDCAVE]

Bennett's page 170:

Still won't let me upload photos!

Jim

[john_tullamarine]

Jim,

You really are making things complicated for yourself. Why not just use the equation for density (from any aerodynamics text) ? Also, the 118.8 ft/C° dev factor is very rough and ready although we routinely use it (actually rounded off to 120) for DH calculations in pilot speak. You may find the following thread on Bob Tait's forum of some use to your deliberations Bob Tait's Aviation Theory School - Altimetry Rates - Bob Tait's Aviation Theory School Forums

So far as posting stuff like graphs, photos, etc., there is a limit which requires you to have a number of posts before the site lets you. I can't remember the figure but it's probably something like 10 posts. In the meantime, if you email stuff to me as attachments, I can put them into your posts in the interim.