A light aircraft will descend faster, so will a heavy one..
Join Date: Apr 2014
Location: Europe
Age: 33
Posts: 142
Likes: 0
Received 0 Likes
on
0 Posts
Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
I want a Blue User Title
Thread Starter
Join Date: Oct 2016
Location: Winterthur
Posts: 166
Likes: 0
Received 0 Likes
on
0 Posts
Gents I understood nothing. 
Either I dust off the books and get to grips with such concepts as drag-curves and LR ratios once again, or someone truly could explain like I am five.

Either I dust off the books and get to grips with such concepts as drag-curves and LR ratios once again, or someone truly could explain like I am five.

Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
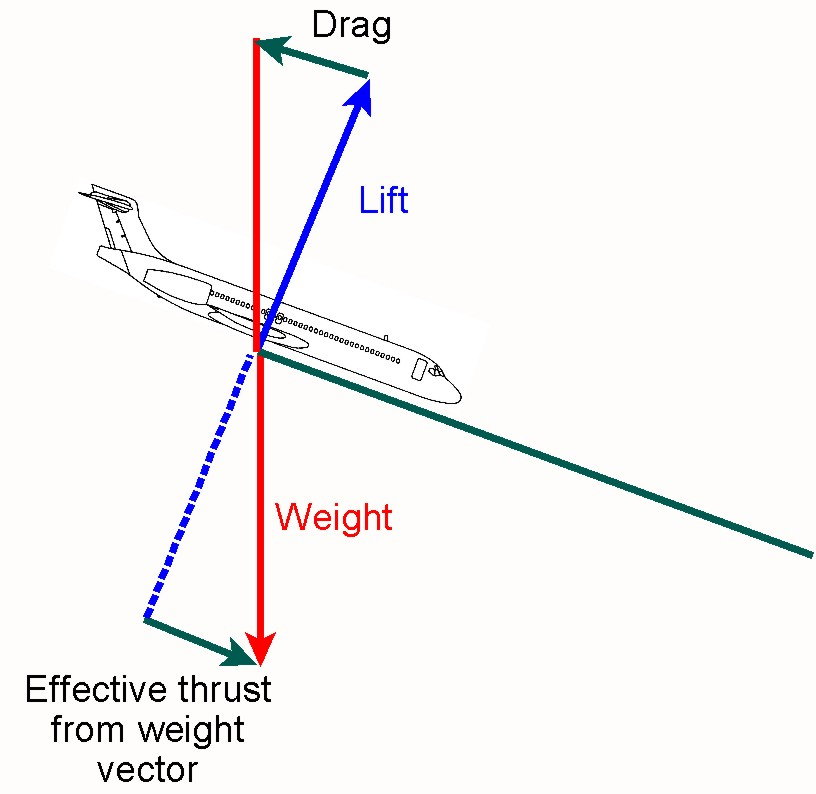
Then, think of a climb or descent. Weight no longer opposes Lift, but is slightly off (by the amount of the climb or descent angle). Due to this off-ness of angle, Weight becomes partially aligned with either Drag (in a climb) or Thrust (in a descent.) In the picture a few posts up, this is represented by the green forward-pointing vector in the bottom triangle. This is called the Forward (if descending, or Rearward if climbing) Component of Weight. Put more simply, going up hill, weight is pulling you back, and if going downhill, weight is pulling you forward. This is the same mechanic as what happens in a car going uphill or downhill. (Literally the same, it’s not an analogy or any other type of mental trick). I bet you already understood this in a common-sense gut level, if not by drawing triangles. This is why you tend to slow down uphill and speed up downhill.
Now, consider two planes descending at the same angle. If everything about them is the same, then their Weight is the same, and their Forward Component of Weight is the same, and their Thrust and Drag are the same, and their speed is the same. Everything. Now, imagine one is heavier. If we keep everything else the same (descent angle, Thrust, Drag) then the one with greater Weight will also have a greater Forward Component of Weight. Therefore it will try to go faster.
But since we want to keep to the same speed as the lighter one (it’s ATC-assigned speed, or it’s Vmo/Mmo, or whatever) and we can’t reduce drag since we’re already at idle, then the only option for the heavier plane is to reduce the descent angle. Once that’s reduced, then the Forward Component of Weight is reduced (and matches the lighter plane again) not because Weight is reduced, but because the descent angle is.
TLDR: Higher weight pulls the aircraft forward harder, and a reduced slope counteracts this effect.
TLDR in math: (gamma, γ, is descent angle) Longitudinal forces in a descent are T + W sin γ forward, balanced by D backward. If speed is constrained to be the same, then D is the same. T is zero (idle) therefore W sin γ must be kept constant. For that, higher W requires lower sin γ, which means lower γ.
Last edited by Vessbot; 8th Apr 2023 at 01:18.
Imagine the heavy aircraft is so heavy that the best glide speed is the same as Vmo. In this case it canít descend steeper than best glide. Now make it a bit lighter, give it a min drag speed of Vmo - 20 knots. Now it can go a little bit faster than best glide and therefore a bit steeper. The lighter it is, the more margin there is between best glide and Vmo, the steeper it will descend at Vmo.
So the lighter aircraft can descend more steeply. The lighter aircraft will also slow down more quickly due to having less momentum.
Now, imagine one is heavier. If we keep everything else the same (descent angle, Thrust, Drag) then the one with greater Weight will also have a greater Forward Component of Weight. Therefore it will try to go faster.
Join Date: Apr 2014
Location: Europe
Age: 33
Posts: 142
Likes: 0
Received 0 Likes
on
0 Posts
I guess it has to do with the level of simplification. My statement is correct as a "first approximation" with simplifying assumptions such as small angles etc. One can always go one step deeper in aerodynamics but a first order of magnitude is good enough here.
I want a Blue User Title
Thread Starter
Join Date: Oct 2016
Location: Winterthur
Posts: 166
Likes: 0
Received 0 Likes
on
0 Posts
Starting from the very basics. Straight and level, unaccelerated flight. Lift opposes Weight, Thrust opposes Drag. Everything is 90 or 180 degrees to everything else.
Then, think of a climb or descent. Weight no longer opposes Lift, but is slightly off (by the amount of the climb or descent angle). Due to this off-ness of angle, Weight becomes partially aligned with either Drag (in a climb) or Thrust (in a descent.) In the picture a few posts up, this is represented by the green forward-pointing vector in the bottom triangle. This is called the Forward (if descending, or Rearward if climbing) Component of Weight. Put more simply, going up hill, weight is pulling you back, and if going downhill, weight is pulling you forward. This is the same mechanic as what happens in a car going uphill or downhill. (Literally the same, itís not an analogy or any other type of mental trick). I bet you already understood this in a common-sense gut level, if not by drawing triangles. This is why you tend to slow down uphill and speed up downhill.
Now, consider two planes descending at the same angle. If everything about them is the same, then their Weight is the same, and their Forward Component of Weight is the same, and their Thrust and Drag are the same, and their speed is the same. Everything. Now, imagine one is heavier. If we keep everything else the same (descent angle, Thrust, Drag) then the one with greater Weight will also have a greater Forward Component of Weight. Therefore it will try to go faster.
But since we want to keep to the same speed as the lighter one (itís ATC-assigned speed, or itís Vmo/Mmo, or whatever) and we canít reduce drag since weíre already at idle, then the only option for the heavier plane is to reduce the descent angle. Once thatís reduced, then the Forward Component of Weight is reduced (and matches the lighter plane again) not because Weight is reduced, but because the descent angle is.
TLDR: Higher weight pulls the aircraft forward harder, and a reduced slope counteracts this effect.
TLDR in math: (gamma, γ, is descent angle) Longitudinal forces in a descent are T + W sin γ forward, balanced by D backward. If speed is constrained to be the same, then D is the same. T is zero (idle) therefore W sin γ must be kept constant. For that, higher W requires lower sin γ, which means lower γ.
Then, think of a climb or descent. Weight no longer opposes Lift, but is slightly off (by the amount of the climb or descent angle). Due to this off-ness of angle, Weight becomes partially aligned with either Drag (in a climb) or Thrust (in a descent.) In the picture a few posts up, this is represented by the green forward-pointing vector in the bottom triangle. This is called the Forward (if descending, or Rearward if climbing) Component of Weight. Put more simply, going up hill, weight is pulling you back, and if going downhill, weight is pulling you forward. This is the same mechanic as what happens in a car going uphill or downhill. (Literally the same, itís not an analogy or any other type of mental trick). I bet you already understood this in a common-sense gut level, if not by drawing triangles. This is why you tend to slow down uphill and speed up downhill.
Now, consider two planes descending at the same angle. If everything about them is the same, then their Weight is the same, and their Forward Component of Weight is the same, and their Thrust and Drag are the same, and their speed is the same. Everything. Now, imagine one is heavier. If we keep everything else the same (descent angle, Thrust, Drag) then the one with greater Weight will also have a greater Forward Component of Weight. Therefore it will try to go faster.
But since we want to keep to the same speed as the lighter one (itís ATC-assigned speed, or itís Vmo/Mmo, or whatever) and we canít reduce drag since weíre already at idle, then the only option for the heavier plane is to reduce the descent angle. Once thatís reduced, then the Forward Component of Weight is reduced (and matches the lighter plane again) not because Weight is reduced, but because the descent angle is.
TLDR: Higher weight pulls the aircraft forward harder, and a reduced slope counteracts this effect.
TLDR in math: (gamma, γ, is descent angle) Longitudinal forces in a descent are T + W sin γ forward, balanced by D backward. If speed is constrained to be the same, then D is the same. T is zero (idle) therefore W sin γ must be kept constant. For that, higher W requires lower sin γ, which means lower γ.
Appreciate everyone's replies here, read them all. Thanks guys for explaining it on a simple level, makes sense now.
Only half a speed-brake
Do you accept that the heavy aircraft and light aircraft both have the same glide ratio but on the heavier aircraft it occurs at a higher speed (min drag speed is higher on the heavy aircraft)? And that flying faster than this speed will increase the descent angle?
Imagine the heavy aircraft is so heavy that the best glide speed is the same as Vmo. In this case it canít descend steeper than best glide. Now make it a bit lighter, give it a min drag speed of Vmo - 20 knots. Now it can go a little bit faster than best glide and therefore a bit steeper. The lighter it is, the more margin there is between best glide and Vmo, the steeper it will descend at Vmo.
So the lighter aircraft can descend more steeply. The lighter aircraft will also slow down more quickly due to having less momentum.
Imagine the heavy aircraft is so heavy that the best glide speed is the same as Vmo. In this case it canít descend steeper than best glide. Now make it a bit lighter, give it a min drag speed of Vmo - 20 knots. Now it can go a little bit faster than best glide and therefore a bit steeper. The lighter it is, the more margin there is between best glide and Vmo, the steeper it will descend at Vmo.
So the lighter aircraft can descend more steeply. The lighter aircraft will also slow down more quickly due to having less momentum.

two identical aircraft, one heavy, one light start a glide at the same place at their own best glide speed. They will reach the ground at exactly the same spot, the heavy one will get there first.
I remember being surprised by that during ATPL theory.
I remember being surprised by that during ATPL theory.
There are two opposing scenarios here.
The theoretical scenario is where aircraft descend at the AOA for best L/D. In this case, a heavy aeroplane will descend on exactly the same path (AOA), but at a greater speed, than a light aircraft. Both will hit the ground at the same point, the only difference being that the heavier aeroplane will hit faster/quicker.
This is eloquently explained by none other than A C Kermode in The Mechanics of Flight, presented to me by my Dad in April 1975 (use my diagram below for the "Fig 6.1" discussion):

The Practical scenario is completely different. That is, we descend at (approximately) the same speed for all descents. We do not descend at Vmin+5 (or Green Dot?). We descend at say Mach 0.8 into 280KIAS. This completely changes the dynamics of the descent. Because the thrust is zero, the only way the aeroplane can counter the drag at the "fixed" speed is to use the weight, by diving. Now, if the aeroplane is heavier, the effective thrust from the weight will be more, and so it doesn't need to descend as steeply as a light aeroplane.
And that's all there is to it.
Scarebus discussion on page 159 here:
https://www.skybrary.aero/bookshelf/...-february-2002
It's "Getting a grip on" or "Coming to grips with"! But then Airbii aren't English are they!
The theoretical scenario is where aircraft descend at the AOA for best L/D. In this case, a heavy aeroplane will descend on exactly the same path (AOA), but at a greater speed, than a light aircraft. Both will hit the ground at the same point, the only difference being that the heavier aeroplane will hit faster/quicker.
This is eloquently explained by none other than A C Kermode in The Mechanics of Flight, presented to me by my Dad in April 1975 (use my diagram below for the "Fig 6.1" discussion):

The Practical scenario is completely different. That is, we descend at (approximately) the same speed for all descents. We do not descend at Vmin+5 (or Green Dot?). We descend at say Mach 0.8 into 280KIAS. This completely changes the dynamics of the descent. Because the thrust is zero, the only way the aeroplane can counter the drag at the "fixed" speed is to use the weight, by diving. Now, if the aeroplane is heavier, the effective thrust from the weight will be more, and so it doesn't need to descend as steeply as a light aeroplane.
And that's all there is to it.

Scarebus discussion on page 159 here:
https://www.skybrary.aero/bookshelf/...-february-2002
It's "Getting a grip on" or "Coming to grips with"! But then Airbii aren't English are they!

A heavy a/c at max landing weight, more distance is required. Takes longer to slow the aircraft down.
Hope that makes sense.
Weight does not effect the glide range within certain parameters. It does effect the TAS. Heavy = Fast.
Last edited by RichardJones; 20th Apr 2023 at 18:54.
Join Date: Jul 2002
Location: Netherlands
Age: 71
Posts: 165
Likes: 0
Received 0 Likes
on
0 Posts
For You as a Swiss guy You will understand next, I will try to keep it as simple as possible.
Driving uphill in a car requires energy. Driving the same car, but now with 4 people on board, requires much more energy. The more people in the car, the more energy needed. Going down, the heavy car will need using the brake much more often than the same, but lighter car.
Weight is "the engine" during descent, to keep the car rolling, the more weight, to more "power" You have. You cannot switch off the "weight engine".
So once two cars are on top of a mountain, the light one has much LESS (potential) energy stored than the same car, with 4 people in it.
But You cannot change the % of slope on a mountain, airplanes CAN change their descent angle.
Example: two identical airplanes, both at 10km of cruising altitude, one at max allowable weight, and the other one, as empty as possible, will have a enormous difference in energy state.
For a normal descent, both will fly at the same SPEED. But the heavy one needs to select a LESS STEEP descent angle, otherwise the excess energy will drive the plane into crazy dangerous speeds. OR it needs to pull the speed brakes (like the car), but that is highly uneconomic.
In the 747 I flew for 22 Years (all types), descent planning was done initially by looking at a simple table: The more WEIGHT You had, the MORE distance You needed to start the descent before destination, in order not to overshoot the destination.
By dusted memory, at a very light weight you needed about 110 Nm before destination, but when You were heavy, it would be 130 NM or so.
Remember, airliners use idle power during descents, so that is not a factor. Here again, weight is the engine that maintains flying speed.
Ik kept out wind influence, difference in gliding performance at different weights, I think those are NOT the factors, TS is looking for.
Modern airliners do the calculation of where would be the optimal TOD (Top Of Descent), that flight, electronically, but it also uses actual weight (together with things like forecasted winds) as the MAIN factors to determine that point.
Richard
Driving uphill in a car requires energy. Driving the same car, but now with 4 people on board, requires much more energy. The more people in the car, the more energy needed. Going down, the heavy car will need using the brake much more often than the same, but lighter car.
Weight is "the engine" during descent, to keep the car rolling, the more weight, to more "power" You have. You cannot switch off the "weight engine".
So once two cars are on top of a mountain, the light one has much LESS (potential) energy stored than the same car, with 4 people in it.
But You cannot change the % of slope on a mountain, airplanes CAN change their descent angle.
Example: two identical airplanes, both at 10km of cruising altitude, one at max allowable weight, and the other one, as empty as possible, will have a enormous difference in energy state.
For a normal descent, both will fly at the same SPEED. But the heavy one needs to select a LESS STEEP descent angle, otherwise the excess energy will drive the plane into crazy dangerous speeds. OR it needs to pull the speed brakes (like the car), but that is highly uneconomic.
In the 747 I flew for 22 Years (all types), descent planning was done initially by looking at a simple table: The more WEIGHT You had, the MORE distance You needed to start the descent before destination, in order not to overshoot the destination.
By dusted memory, at a very light weight you needed about 110 Nm before destination, but when You were heavy, it would be 130 NM or so.
Remember, airliners use idle power during descents, so that is not a factor. Here again, weight is the engine that maintains flying speed.
Ik kept out wind influence, difference in gliding performance at different weights, I think those are NOT the factors, TS is looking for.
Modern airliners do the calculation of where would be the optimal TOD (Top Of Descent), that flight, electronically, but it also uses actual weight (together with things like forecasted winds) as the MAIN factors to determine that point.
Richard
Originally Posted by Richard Jones
Weight does not effect the glide range within certain parameters. It does effect the TAS. Heavy = Fast.
Weight has a direct effect on the "gliding" aka idle-thrust descent range because we are descending at the same speed. The higher the weight, the more descent distance a jet needs at the ATC speed.
Incorrect. That is what the thread is all about. Doubleback's explanation is spot-on.
Weight has a direct effect on the "gliding" aka idle-thrust descent range because we are descending at the same speed. The higher the weight, the more descent distance a jet needs at the ATC speed.
Weight has a direct effect on the "gliding" aka idle-thrust descent range because we are descending at the same speed. The higher the weight, the more descent distance a jet needs at the ATC speed.
A lot of theories but trust me as I got 16,700 fpm out of an empty F100 going into Rome before I chickened out and was still a good 30 knots below VNE whilst looking at the terrain below us..wasn’t popular with the crew…
Join Date: Feb 2001
Location: Milkway Galaxy
Posts: 240
Likes: 0
Received 0 Likes
on
0 Posts
“If you can’t explain it to a six-year-old, then you don’t understand it yourself” Albert Einstein
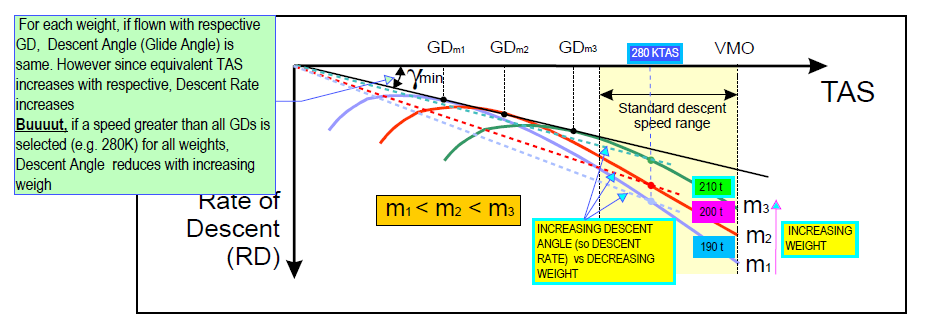
Following figure is extracted from AIRBUS Getting the Grips with Aircraft Performance P 163 (attached note boxes are mine)
Commented as:
1. For different weights, if respective Green Dot (GD) speed is maintained, Descent Angle (DA, in another word Glide Path Angle, GPA,) and Descent Range remains same; however with increasing weight, Rate of Descent (RD) increases or vice versa
2. For all different weights, if a fixed (same) speed value, within Standard Descent Speed Range (eg 280K), is maintained, as weight increases, DA (=GPA) and RD decreases, consequently Descent Range increases
3. A counter-intuitive point: Why DA (=GPA) decreases with increasing weight?
ANSWER: During glide, the drag along flight path is balanced with the component of weight along flight path, in the opposite direction with drag. Therefore, as weight increases, less GPA (=DA) becomes enough to counter drag; result is less RD
Full stop
NOTE I have a thread titled "AMC3 CAT.OP.MPA.182 Fuel/energy scheme — aerodrome selection policy — aeroplanes" I need some comments and replies please
Thanks
Last edited by JABBARA; 21st Apr 2023 at 20:47. Reason: My poor English
Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
Incorrect. That is what the thread is all about. Doubleback's explanation is spot-on.
Weight has a direct effect on the "gliding" aka idle-thrust descent range because we are descending at the same speed. The higher the weight, the more descent distance a jet needs at the ATC speed.
Weight has a direct effect on the "gliding" aka idle-thrust descent range because we are descending at the same speed. The higher the weight, the more descent distance a jet needs at the ATC speed.
If speed is unconstrained, then best glide angle is the same at all weights. But at a higher weight, that best glide angle is achieved at a higher speed.
If speed is constrained to a certain number, then glide angle (not best, just glide angle) is shallower at a higher weight.
Join Date: Feb 2001
Location: Milkway Galaxy
Posts: 240
Likes: 0
Received 0 Likes
on
0 Posts
Pugilistic Animus
Correct if you fly with (L/D)max speed (=GD) of each weight.
Otherwise, if you fly faster but same speed for any weight, the heavier has more range.
The heavier plane at glide speed will reach the same position as a lighter plane, only faster...if a made an error don't crucify me 

Otherwise, if you fly faster but same speed for any weight, the heavier has more range.