A light aircraft will descend faster, so will a heavy one..
I want a Blue User Title
Thread Starter
Join Date: Oct 2016
Location: Winterthur
Posts: 166
Likes: 0
Received 0 Likes
on
0 Posts
A light aircraft will descend faster, so will a heavy one..
Please, like I am a five-year-old child can someone explain this.
A heavy aircraft will descend faster because of the momentum it has.
A light aircraft will descend faster because it can reach a higher speed, less limited by VMO/MMO on the descent.
So which one is the truth, do you need to plan more track miles to descend a heavier aircraft or a lighter aircraft?
Additionally in terms of slowing down, which do you need to plan more track miles for? A lighter aircraft will take time to slow down due to its inertia. But a heavier aircraft will also take time to slow down because of its momentum, sometimes you need to drop the gear for example.
Would appreciate any underlying logic. Thank you.
A heavy aircraft will descend faster because of the momentum it has.
A light aircraft will descend faster because it can reach a higher speed, less limited by VMO/MMO on the descent.
So which one is the truth, do you need to plan more track miles to descend a heavier aircraft or a lighter aircraft?
Additionally in terms of slowing down, which do you need to plan more track miles for? A lighter aircraft will take time to slow down due to its inertia. But a heavier aircraft will also take time to slow down because of its momentum, sometimes you need to drop the gear for example.
Would appreciate any underlying logic. Thank you.
Last edited by k.swiss; 3rd Apr 2023 at 15:07. Reason: Added part about slowing down.
Is this the same aircraft at two different load states?
Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
Please, like I am a five-year-old child can someone explain this.
A heavy aircraft will descend faster because of the momentum it has.
A light aircraft will descend faster because it can reach a higher speed, less limited by VMO/MMO on the descent.
So which one is the truth, do you need to plan more track miles to descend a heavier aircraft or a lighter aircraft?
A heavy aircraft will descend faster because of the momentum it has.
A light aircraft will descend faster because it can reach a higher speed, less limited by VMO/MMO on the descent.
So which one is the truth, do you need to plan more track miles to descend a heavier aircraft or a lighter aircraft?
However, a heavier airplane (at the same speed as a lighter one) is closer to its (L/D)max speed, and therefore will glide at a shallower angle.
(Remember, as a baseline, that they have the same (L/D)max, yielding the same glide angle, but the heavier one occurs at a faster speed, and higher descent rate.)
"A heavy aircraft will descend faster" is incorrect - they are capable of not descending at all until the fuel runs out and the engines are running. Momentum has nothing to with that. A plane heavy with fuel will do this for a longer time.
If the engines stop, then the best glide (for distance) speed will be higher for the heavier state because the lift requirement will be higher making the drag higher and therefore the greater rate required for turning altitude into kinetic energy to be bled off via drag. AFAIK the distance will be the same.
If the engines stop, then the best glide (for distance) speed will be higher for the heavier state because the lift requirement will be higher making the drag higher and therefore the greater rate required for turning altitude into kinetic energy to be bled off via drag. AFAIK the distance will be the same.
Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
Additionally in terms of slowing down, which do you need to plan more track miles for? A lighter aircraft will take time to slow down due to its inertia. But a heavier aircraft will also take time to slow down because of its momentum, sometimes you need to drop the gear for example.
Inertia and momentum functionally mean the same thing here, and the heavier plane has more of it; and will take more time and distance to slow down because of it.
Join Date: Apr 2014
Location: Europe
Age: 33
Posts: 142
Likes: 0
Received 0 Likes
on
0 Posts
What you are looking at is the descent angle (gamma) which is a function of the lift to drag ratio L/D.
As a first approximation, the aircraft with the higher L/D will descend at a shallower angle and will need more track miles to descend.
As a first approximation, the aircraft with the higher L/D will descend at a shallower angle and will need more track miles to descend.
Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
OK, and which aircraft has a higher L/D?
Join Date: Apr 2014
Location: Europe
Age: 33
Posts: 142
Likes: 0
Received 0 Likes
on
0 Posts
Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
Join Date: Apr 2014
Location: Europe
Age: 33
Posts: 142
Likes: 0
Received 0 Likes
on
0 Posts
Well then the limitation becomes the Vmo. Assuming Vmo is a fixed number independent of mass, both aircraft descend at the same IAS, the heavier one should have a higher L/D ratio (more lift for the same amount of drag) and therefore a shallower descent angle (more track miles).
Join Date: May 1999
Location: Bristol, England
Age: 65
Posts: 1,805
Received 0 Likes
on
0 Posts
This sounds like something out of the ATPL theory which is based in turn on the pre-war work on gliding theory. You balance the static forces in the descent and derive a formula that says sin gamma = (drag-thrust)/weight. You observe thrust is minimal so say that sin gamma = drag/weight, and then observe that, assuming weight is relatively constant, the smallest value of sin gamma occurs where the drag is least and make the first statement that the most shallow glide angle occurs if you fly at VMD for the weight.
Now hop back to the previous formula that says sin gamma = drag/weight and substitute CD/CL for drag/weight, this leads to the second statement that the glide angle is the lift drag ratio upside down, and this is independent of weight provided you fly at the correct VMD for that weight. Now we have statement #3 which is that, provided you fly at the correct VMD for the weight, the glide angle (flight path angle) will be the same for both a heavy aircraft or a light aircraft and therefore, in answer to the OP's question, the planned track miles will be the same.
Now rate of descent, and for this you need a dynamic diagram with a right angle triangle with descent angle gamma, TAS on the hypotenuse and rate of descent in the vertical. sin gamma = O/H = rate of descent / TAS, therefore rate of descent = Sin gamma x TAS. The heavier aircraft will have the same sin gamma in a VMD glide but IAS will be higher, so TAS will be higher, so rate of descent will be higher. Now we have statement #4 which develops from #3, which is that, provided you fly at the correct VMD for the weight, the glide angle (flight path angle) will be the same for both a heavy aircraft or a light aircraft but the heavier aircraft will have a higher TAS and therefore a higher rate of descent.
Now hop back to the previous formula that says sin gamma = drag/weight and substitute CD/CL for drag/weight, this leads to the second statement that the glide angle is the lift drag ratio upside down, and this is independent of weight provided you fly at the correct VMD for that weight. Now we have statement #3 which is that, provided you fly at the correct VMD for the weight, the glide angle (flight path angle) will be the same for both a heavy aircraft or a light aircraft and therefore, in answer to the OP's question, the planned track miles will be the same.
Now rate of descent, and for this you need a dynamic diagram with a right angle triangle with descent angle gamma, TAS on the hypotenuse and rate of descent in the vertical. sin gamma = O/H = rate of descent / TAS, therefore rate of descent = Sin gamma x TAS. The heavier aircraft will have the same sin gamma in a VMD glide but IAS will be higher, so TAS will be higher, so rate of descent will be higher. Now we have statement #4 which develops from #3, which is that, provided you fly at the correct VMD for the weight, the glide angle (flight path angle) will be the same for both a heavy aircraft or a light aircraft but the heavier aircraft will have a higher TAS and therefore a higher rate of descent.
That's all well and good, but we're not flying at VMD we're trying to fly a steep descent which means at Vmo / Mmo. At Vmo / Mmo a heavy aircraft is closer to its VMD and will have a better glide than the light aircraft. It's quite obvious in practice when flying older jets without VNAV.
Well then the limitation becomes the Vmo. Assuming Vmo is a fixed number independent of mass, both aircraft descend at the same IAS, the heavier one should have a higher L/D ratio (more lift for the same amount of drag) and therefore a shallower descent angle (more track miles).
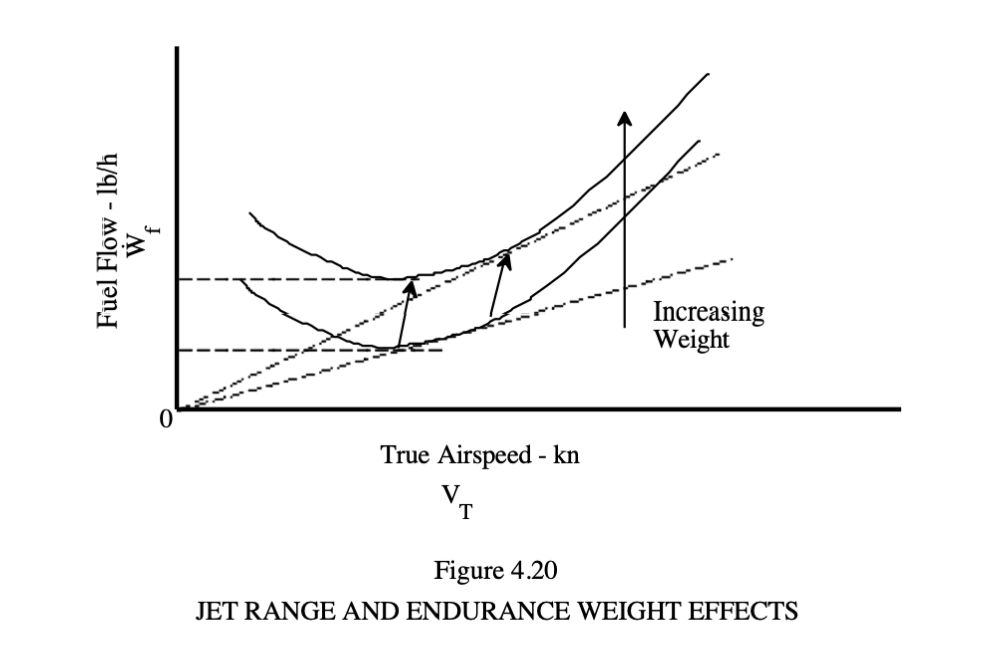
Have a look at this chart, and then perhaps consider your statement. You are around 90% there, but that means a 100% review.
Consider first level flight at a constant AOA; total lift variables for a comparison are Lift =CL.V^2, that's the set of variables. everything else is lipgloss in a comparative analysis. So, as Lift must equal weight for level flight, the heavier aircraft must either have a higher CL for a constant speed, or an increased speed for a constant CL. CL is related to the a-slope of CL v AOA. In general the relationship of almost all systems will be around 0.09 CL for every degree of AOA. There are a few things that will affect that, such as aspect ratio, and very slightly VGs can increase that slope... trailing edge mods may also increase that slope.
So, thinking laterally from that case, consider when the aircraft is in a straight glide.. the chart will get you to your journey.
May the forces be with you
Airlines usually have published descent profiles which are more or less independent of weight.
Within these parameters a heavy aircraft takes more track miles for descent coz it has more energy to dissipate.
On B744, in my experience, it's not a big deal coz of winds and ATC vectoring. Use the Perf manual figures and you won't be too far wrong then patch it up.
Within these parameters a heavy aircraft takes more track miles for descent coz it has more energy to dissipate.
On B744, in my experience, it's not a big deal coz of winds and ATC vectoring. Use the Perf manual figures and you won't be too far wrong then patch it up.
There are two opposing scenarios here.
The theoretical scenario is where aircraft descend at the AOA for best L/D. In this case, a heavy aeroplane will descend on exactly the same path (AOA), but at a greater speed, than a light aircraft. Both will hit the ground at the same point, the only difference being that the heavier aeroplane will hit faster/quicker.
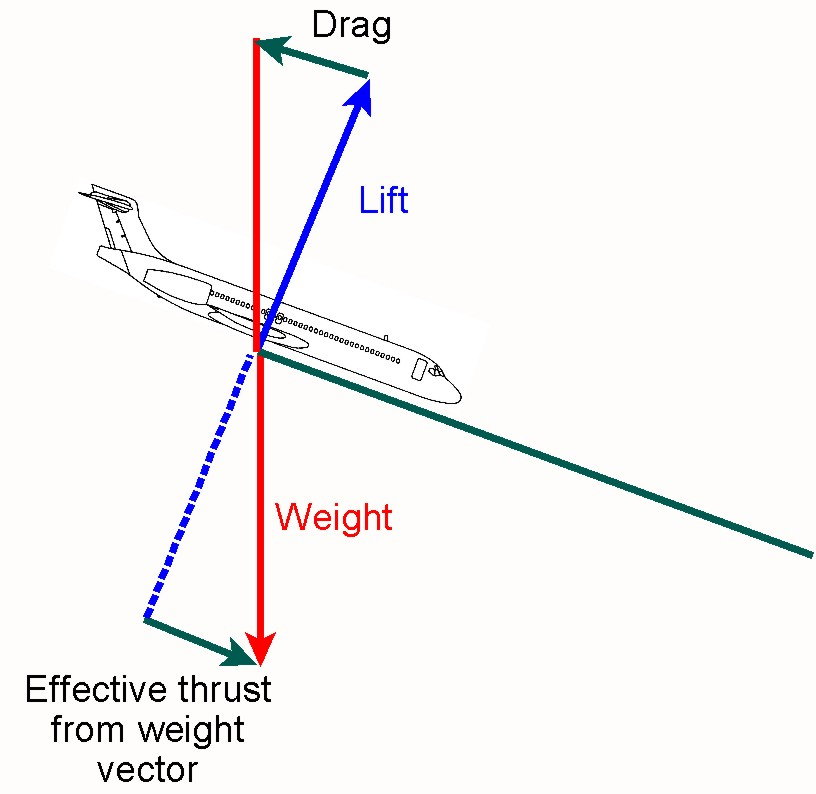
This is eloquently explained by none other than A C Kermode in The Mechanics of Flight, presented to me by my Dad in April 1975 (use my diagram below for the "Fig 6.1" discussion):

The Practical scenario is completely different. That is, we descend at (approximately) the same speed for all descents. We do not descend at Vmin+5 (or Green Dot?). We descend at say Mach 0.8 into 280KIAS. This completely changes the dynamics of the descent. Because the thrust is zero, the only way the aeroplane can counter the drag at the "fixed" speed is to use the weight, by diving. Now, if the aeroplane is heavier, the effective thrust from the weight will be more, and so it doesn't need to descend as steeply as a light aeroplane.
And that's all there is to it.
Scarebus discussion on page 159 here:
https://www.skybrary.aero/bookshelf/...-february-2002
It's "Getting a grip on" or "Coming to grips with"! But then Airbii aren't English are they!
The theoretical scenario is where aircraft descend at the AOA for best L/D. In this case, a heavy aeroplane will descend on exactly the same path (AOA), but at a greater speed, than a light aircraft. Both will hit the ground at the same point, the only difference being that the heavier aeroplane will hit faster/quicker.
This is eloquently explained by none other than A C Kermode in The Mechanics of Flight, presented to me by my Dad in April 1975 (use my diagram below for the "Fig 6.1" discussion):

The Practical scenario is completely different. That is, we descend at (approximately) the same speed for all descents. We do not descend at Vmin+5 (or Green Dot?). We descend at say Mach 0.8 into 280KIAS. This completely changes the dynamics of the descent. Because the thrust is zero, the only way the aeroplane can counter the drag at the "fixed" speed is to use the weight, by diving. Now, if the aeroplane is heavier, the effective thrust from the weight will be more, and so it doesn't need to descend as steeply as a light aeroplane.
And that's all there is to it.

Scarebus discussion on page 159 here:
https://www.skybrary.aero/bookshelf/...-february-2002
It's "Getting a grip on" or "Coming to grips with"! But then Airbii aren't English are they!

Join Date: Sep 2016
Location: USA
Posts: 803
Likes: 0
Received 0 Likes
on
0 Posts
So which one is the truth, do you need to plan more track miles to descend a heavier aircraft or a lighter aircraft?
If you descend at the same speed in both, then you will need more track miles in the heavier aircraft. Simple explanation: best L/D speed increases with wing loading, so your glide angle will be better in the heavier aircraft == more miles.
Additionally in terms of slowing down, which do you need to plan more track miles for? A lighter aircraft will take time to slow down due to its inertia. But a heavier aircraft will also take time to slow down because of its momentum, sometimes you need to drop the gear for example.
Additionally in terms of slowing down
Again, a heavier aircraft needs more track miles.
Certainly though, from the same point in the sky, say 5000ft at 20nm at 250KIAS, a heavier aircraft will take longer to slow down than a lighter one for the reason I showed above: the longer/larger weight vector contributes more to the effective thrust, meaning that either the heavier will glide further or, if forced onto the same flightpath eg 5000ft/20nm to 3000/10nm, it won't slow down as much.



