Physics of falling objects
Oh dear do I have to repeat myself. I am asking for someone to explain this variable gravity theory of tides. If you can, fine, please do. If you can't I'll continue to wait.
Join Date: Dec 2012
Location: nowhere
Posts: 151
Likes: 0
Received 0 Likes
on
0 Posts
A Squared
You are partially right! Before I take the discussion any further I'd like you to answer the following question;
2 objects same dimensions etc but different masses, 1 say 1kg the other 10 kg with both being dropped say 10m, will they hit the the same time or will the heavier one hit first?
2 objects same dimensions etc but different masses, 1 say 1kg the other 10 kg with both being dropped say 10m, will they hit the the same time or will the heavier one hit first?
Join Date: Feb 2000
Location: Alaska, PNG, etc.
Age: 60
Posts: 1,550
Likes: 0
Received 0 Likes
on
0 Posts
You are partially right! Before I take the discussion any further I'd like you to answer the following question;
2 objects same dimensions etc but different masses, 1 say 1kg the other 10 kg with both being dropped say 10m, will they hit the the same time or will the heavier one hit first?
2 objects same dimensions etc but different masses, 1 say 1kg the other 10 kg with both being dropped say 10m, will they hit the the same time or will the heavier one hit first?
Join Date: Feb 2000
Location: Alaska, PNG, etc.
Age: 60
Posts: 1,550
Likes: 0
Received 0 Likes
on
0 Posts
Well, Tides are a result of temporal variations in the net gravitational acceleration vector caused by the effects of the moon and sun. But, I suspect that you know that and are merely trying to start an argument based on the use of imprecise terms. Knock yourself out.
Join Date: Dec 2012
Location: nowhere
Posts: 151
Likes: 0
Received 0 Likes
on
0 Posts
A Squared
Well. A Squared, you'd be wrong.
After your first response I went and paid a visit to a young lady (physics grad) who tutored my daughter in Physics a couple of years back.
S = ut + 1/2 at^
^ = squared
She said this is the valid equation up until the point the object reaches Vt, as the object is still accelerating and mass does not come into it, so in a fall where the objects fail to reach their Vt the above equation is it and they will hit the ground at the same time. Now, if the distance the objects fall is such that Vt will be reach prior to their hitting the ground the Vt equation of
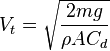 will come into it. At this point mass impacts Vt and therefor the higher mass object will have a higher Vt and will hit the ground earlier. So the as the lighter object reaches Vt (now falls at its Vt as determined by the Vt equation) it will now stop accelerating while the higher mass object continues to accelerate (using s =ut +1/2 at^), until it reaches Vt.
will come into it. At this point mass impacts Vt and therefor the higher mass object will have a higher Vt and will hit the ground earlier. So the as the lighter object reaches Vt (now falls at its Vt as determined by the Vt equation) it will now stop accelerating while the higher mass object continues to accelerate (using s =ut +1/2 at^), until it reaches Vt.
So as to the effect of mass depends on whether the object hits the ground prior to reaching Vt.
She laughed at your helium balloon comparison, if you check a reasonable link the Vt equation like at this link
Terminal velocity - Wikipedia, the free encyclopedia
you'll see it mentions where buoyancy isn't a consideration.
Mass comes into the Vt equation as it's "pushing" against the air resistance, thus a higher mass object will have a higher Vt.
After your first response I went and paid a visit to a young lady (physics grad) who tutored my daughter in Physics a couple of years back.
S = ut + 1/2 at^
^ = squared
She said this is the valid equation up until the point the object reaches Vt, as the object is still accelerating and mass does not come into it, so in a fall where the objects fail to reach their Vt the above equation is it and they will hit the ground at the same time. Now, if the distance the objects fall is such that Vt will be reach prior to their hitting the ground the Vt equation of
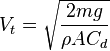 will come into it. At this point mass impacts Vt and therefor the higher mass object will have a higher Vt and will hit the ground earlier. So the as the lighter object reaches Vt (now falls at its Vt as determined by the Vt equation) it will now stop accelerating while the higher mass object continues to accelerate (using s =ut +1/2 at^), until it reaches Vt.
will come into it. At this point mass impacts Vt and therefor the higher mass object will have a higher Vt and will hit the ground earlier. So the as the lighter object reaches Vt (now falls at its Vt as determined by the Vt equation) it will now stop accelerating while the higher mass object continues to accelerate (using s =ut +1/2 at^), until it reaches Vt.So as to the effect of mass depends on whether the object hits the ground prior to reaching Vt.
She laughed at your helium balloon comparison, if you check a reasonable link the Vt equation like at this link
Terminal velocity - Wikipedia, the free encyclopedia
you'll see it mentions where buoyancy isn't a consideration.
Mass comes into the Vt equation as it's "pushing" against the air resistance, thus a higher mass object will have a higher Vt.
Buoyancy a consideration?
From YOUR link-
and latter-
So, what you've done is use on equation that doesn't take all aspects of the situation into account.
Applying THAT principle will show that the less dense object will accelerate slower at the outset, so the two objects will NEVER fall at the same rate.
From YOUR link-
The terminal velocity of a falling object is the velocity of the object when the sum of the drag force (Fd) and buoyancy equals the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration.[
Buoyancy effects, due to the upward force on the object by the surrounding fluid, can be taken into account using Archimedes' principle: the mass m has to be reduced by the displaced fluid mass \rho\mathcal{V}, with \mathcal{V} the volume of the object. So instead of m use the reduced mass m_r=m-\rho\mathcal{V} in this and subsequent formulas.
Applying THAT principle will show that the less dense object will accelerate slower at the outset, so the two objects will NEVER fall at the same rate.
Join Date: Dec 2007
Location: Pasadena
Posts: 633
Likes: 0
Received 0 Likes
on
0 Posts
Mr Optimistic,
Tides on Earth are caused by the minor influence of the Sun and (mostly the) Moon's gravity. When Moon is directly overhead, there's a little less net attraction of the water surface to the center of the Earth, and so there's a tidal bulge. Six hours later, there's a sideways pull from the Moon instead, and no such bulge. The gravitational field varies and shifts direction slightly at the Earth's rotation rate.
The bulge opposite the Moon needs you to shift into the rotating frame around the Earth-Moon system center of mass, and is less amenable to a one-line explanation.
Tides on Earth are caused by the minor influence of the Sun and (mostly the) Moon's gravity. When Moon is directly overhead, there's a little less net attraction of the water surface to the center of the Earth, and so there's a tidal bulge. Six hours later, there's a sideways pull from the Moon instead, and no such bulge. The gravitational field varies and shifts direction slightly at the Earth's rotation rate.
The bulge opposite the Moon needs you to shift into the rotating frame around the Earth-Moon system center of mass, and is less amenable to a one-line explanation.
Join Date: Dec 2007
Location: Pasadena
Posts: 633
Likes: 0
Received 0 Likes
on
0 Posts
oggers,
The poor guy's written a decidedly mediocre conference proceeding that advances Mr Stokes' work from the 19th century not one jot.
If you can't see that, then you need more than a hundred-word comment to explain.
I'm not the referee, and professional courtesy would indicate that he not be needlessly harangued. There's nothing grossly incorrect in the paper, but it's neither novel nor insightful. By including unnecessary terms in the gravity, and ignoring the larger degree of ignorance about the density profile, and lift effects, it's not very helpful to the discussion about falling objects.
The poor guy's written a decidedly mediocre conference proceeding that advances Mr Stokes' work from the 19th century not one jot.
If you can't see that, then you need more than a hundred-word comment to explain.
I'm not the referee, and professional courtesy would indicate that he not be needlessly harangued. There's nothing grossly incorrect in the paper, but it's neither novel nor insightful. By including unnecessary terms in the gravity, and ignoring the larger degree of ignorance about the density profile, and lift effects, it's not very helpful to the discussion about falling objects.
Join Date: Dec 2007
Location: Pasadena
Posts: 633
Likes: 0
Received 0 Likes
on
0 Posts
ANCPER,
Your young female friend has either been misinterpreted, or she was giving your daughter a sketchy outline of reality.
The terminal velocity is a limiting value at constant density, so to say that the path is quadratic until you hit the terminal velocity is just not right.
Quadratic distance vs time only applies with zero drag. As density increases, it drops, look at that Austrian balloon skydiver guy.
Your young female friend has either been misinterpreted, or she was giving your daughter a sketchy outline of reality.
The terminal velocity is a limiting value at constant density, so to say that the path is quadratic until you hit the terminal velocity is just not right.
Quadratic distance vs time only applies with zero drag. As density increases, it drops, look at that Austrian balloon skydiver guy.
Join Date: Feb 2000
Location: Alaska, PNG, etc.
Age: 60
Posts: 1,550
Likes: 0
Received 0 Likes
on
0 Posts
Well, ANCPERS, no, I'm not.
It is interesting how you have changed your claim as you've been unable to defend it and you've had to walk it back, so to speak, to avoid admitting you were wrong.
You began by claiming:
But now you're claiming that:
Which means you were wrong. QED.
Of course in order to avoid merely saying “yeah, I was wrong, I was talking out of my nether regions” you've concocted some new fallacy. Now you're claiming that the objects fall at precisely the same rate until the less dense one reaches it's terminal velocity and the more dense one leaves it behind.
It's a more complex fallacy, but every bit as incorrect as your initial fallacy, which you've now abandoned.
A word about your “physics expert” She may well be a physics grad student, but that doesn't mean that she necessarily understands ballistics very well. That would be a subject that physics and engineering students learn in the first semester physics class in their freshman year. Second semester physics has moved on to other subjects. The thing is, Newtonian physics is pretty basic stuff and a physics student, even an undergrad moves on to other more advanced physics pretty quickly. By the time one is in in a physics graduate program, the motion of falling objects is something that they may not have considered in any depth since the first semester of their freshman year. (The astute reader will at this point be wondering: Hmmm, I wonder how A Squared knows about studying physics at a university?)
Of course it is entirely possible that she understands it perfectly well, but you just didn't understand her explanation of it, perhaps willfully on a subconscious level because of your demonstrated desire to not admit you're mistaken.
Regardless, whether it's because she doesn't understand the physics or because you didn’t understand her explanation, either way, the end result is the same; what you've taken away from that conversation is wrong.
Uhhh, nobody mentioned helium balloons. The comparison was air filled balloons (which will fall down). You made up the part about helium. FWIW, the force of buoyancy on an air filled balloon and one filled with concrete is exactly the same. The only difference is that with air filled balloon, the buoyancy is large compared to the weight of the balloon, and small compared to the weight of the concrete filled one, but in either case the force of buoyancy that the air is exerting on the balloons is the same. And as far as the your link goes, you apparently missed the fact that your link is the same one I linked in my previous response to you, and discussed the information therein. Go back and look, it's still there in my post, the second link.
Now, here's why the current iteration of your theory is wrong. You claim that drag makes absolutely no difference until one object reaches it's terminal velocity, at which point it stops accelerating and the other continues accelerating, thus pulling “ahead” and falling faster.
In order to believe that, you'd have to believe that drag is completely non-existent until one object reaches terminal velocity.
OK, let's work through a simple example: Assume a 1 kg object and a 10kg object. The weights of the object (the force of gravity pulling on them) will be 9.8 newtons and 98 newtons respectively.
Let's further assume that the terminal velocity of the heavier object will be 50 m/s. If that is true, and the objects are externally identical (same shape, drag coefficient and frontal area) then the lighter object will reach terminal velocity at about 15.8 m/s
So at 15.8 meters/sec the force of drag (on both objects) will be 9.8 newtons. The lighter one will stop accelerating because that is equal to the force of gravity on the object and the forces cancel each other out, there is no extra force to accelerate the object. That's the definition of terminal velocity, where the force of gravity is exactly balanced by the force of drag. The heavier object will continue to accelerate because the force of drag is 9.8 newtons, but the force of gravity is 98 newtons, so there is still 88.2 newtons accelerating the object.
OK, that's just an explanation of what terminal velocity is. Now your claim is that up till the point that the lighter object reaches terminal velocity, the objects will fall with identical acceleration, thus identical speed, and will reach any point at the identical same time (short of the lighter one reaching terminal velocity)
You're wrong. Here's why: Using our example, at the instant they are released, both objects will begin accelerating at the same rate. There is no motion yet, so drag is zero, non-existent. The only force on the objects is the force of gravity. There is 9.8 newtons of gravitational force acting on the 1 kg mass which causes it to accelerate at 9.8 meters/sec/sec and there is 98 newtons of gravitational force acting on the 10 kg. mass, causing it to also accelerate at 9.8 meters/sec/sec.
That is at the instant of release, when velocity is zero, thus drag is zero, acceleration will be the same.
The thing is, drag does not remain at zero. As the speed increases, so does the drag. What is the drag when the objects are falling at half the lighter object's terminal velocity? Well, it will not be half, because drag is a function of the square of the speed. Half the lighter object's terminal velocity is 7.9 meters/sec. At that speed the drag on both objects will be 2.4 newtons. At that point in the fall, will they both be falling and accelerating at the same speed? Your claim is that they will. You are wrong. We only have to calculate the acceleration at that point to see why you're wrong. At that point, drag on both is 2.4 newtons. That means the the unopposed force on the lighter object will be 9.8 newtons of gravity – 2.4 newtons of drag, or 7.4 newtons. This means that at that point the lighter object will be accelerating at 7.4 meter/sec/sec (7.4 newtons divided by 1 kg) But the unopposed force on the heavier object will be 98 newtons of gravity – 2.4 newtons of drag, or 95.6 newtons. If you apply 95.6 newtons of force to a 10 kg object, the object will accelerate at 9.56 meters/sec/sec.
So, halfway to the lighter object's terminal velocity (in time, not distance), the lighter object is accelerating at 7.5 m/sec/sec, and the heavier one will be accelerating at 9.56 meters/sec/sec. Obviously, if one object is accelerating at a greater rate than the other, they can't possibly maintain the same velocity. And that's just a snapshot of what's happening at one instant in time. The only time the acceleration of the objects has been equal is at the precise moment of release, when velocity as zero, and thus drag was zero. At any instant after the objects have started falling, the acceleration of the heavier object will be greater than the lighter object, because of drag.
Now, I don't expect you to agree. It is clear that your brain is so tied up in the effort of not admitting that you're wrong, that you're unable to follow the explanation.
Here's what you should do. Print this entire discussion out, and take it to your physics grad student friend. Seriously, print it out, don't “explain” it too her, because you clearly don't understand it yourself, and thus are unable to describe it accurately, plus you can't seem to resist making up fictional details like helium balloons, which were not a part of the discussion. Like I said, print it all out without editing it, and hand it to her, and ask her to take it home and read it and think about it.
One of two things is going to happen:
1) she's going to immediately say, “no you misunderstood what I was saying, they do not fall with exact same identical speed until one reaches it's terminal velocity, that's not what I said.
or
2) she will, after having read and considered the explanation , say, yep sorry, I told you incorrectly, the objects will not fall at the same speed until one reaches terminal velocity.
Of course, you could save everyone a lot of effort by just admitting you were wrong. This is painfully obvious to everyone at this point, but I don't think there's any chance you're going to do that. For you it has obviously become a game of: "don't ever admit I was wrong" instead of "I want to understand this better"
Last edited by A Squared; 14th Mar 2014 at 10:03.
Join Date: Feb 2000
Location: Alaska, PNG, etc.
Age: 60
Posts: 1,550
Likes: 0
Received 0 Likes
on
0 Posts
ANCPERS,
Here's another question for your physics grad student. Print it out and give it to her verbatim.
Assume that the terminal velocity of the lighter object is exactly 15.80 m/sec.
What will be the lighter object's acceleration when it is falling at 15.75 m/sec?
If you say it's acceleration is 9.8 m/sec/sec, how can aerodynamic drag be large enough to completely stop acceleration when the speed is 15.80 m/sec, yet have absolutely *no* effect on acceleration when it is falling 0.05 m/sec slower?
If you say that the acceleration will be less than 9.8 m/sec/sec, then *why* is it not accelerating at exactly g (9.8m/sec/sec) ?
Here's another question for your physics grad student. Print it out and give it to her verbatim.
Assume that the terminal velocity of the lighter object is exactly 15.80 m/sec.
What will be the lighter object's acceleration when it is falling at 15.75 m/sec?
If you say it's acceleration is 9.8 m/sec/sec, how can aerodynamic drag be large enough to completely stop acceleration when the speed is 15.80 m/sec, yet have absolutely *no* effect on acceleration when it is falling 0.05 m/sec slower?
If you say that the acceleration will be less than 9.8 m/sec/sec, then *why* is it not accelerating at exactly g (9.8m/sec/sec) ?
Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
ANCPER
He is not wrong.
She is wrong. That is not the correct equation to use with drag - not even "up until terminal velocity". She is correct about the terminal velocity though, which is just a rearrangement (in the special case where Fnet = 0) of the equation:
Fnet = mg - (Cd x ½ρv²s)
From this equation you should be able to see that for any velocity, if the mass is higher, Fnet is higher.
Well. A Squared, you'd be wrong
After your first response I went and paid a visit to a young lady (physics grad) who tutored my daughter in Physics a couple of years back.
S = ut + 1/2 at^
^ = squared
She said this is the valid equation up until the point the object reaches Vt, as the object is still accelerating and mass does not come into it, so in a fall where the objects fail to reach their Vt the above equation is it and they will hit the ground at the same time.
S = ut + 1/2 at^
^ = squared
She said this is the valid equation up until the point the object reaches Vt, as the object is still accelerating and mass does not come into it, so in a fall where the objects fail to reach their Vt the above equation is it and they will hit the ground at the same time.
Fnet = mg - (Cd x ½ρv²s)
From this equation you should be able to see that for any velocity, if the mass is higher, Fnet is higher.
Join Date: Jan 2001
Location: Home
Posts: 3,399
Likes: 0
Received 0 Likes
on
0 Posts
awblain
"And tourist, perhaps a remedial course in counting is in order, or am I somehow wrong about the intertidal period and the oceanic tidal range? "
"The tidal acceleration moves water about two meters in six hours.
The free fall acceleration moves water two meters in about 0.4 seconds.
The force is related to the square of the ratio of those times. That's gives a measure of the low-down scale of tidal forces"
No.
The force that moves tides is not that simple. If it were, then lakes would go up and down in a similar range. They don't incidentally.
If you drop water in free fall, then it can fall because there is obviously nothing underneath it.
The sea is not in that position. For the surface to rise and fall, the water has to move sideways, or the water has to expand and contract.
The example you quoted of a tidal range of 2m in 6 hours is not a simple F=ma equation.
You have to bring in an incredibly complex range of factors including sea bottom shape, sea viscosity, flow patterns through constrictions, compressibility to name just the first ones off the top of my head.
"And tourist, perhaps a remedial course in counting is in order, or am I somehow wrong about the intertidal period and the oceanic tidal range? "
"The tidal acceleration moves water about two meters in six hours.
The free fall acceleration moves water two meters in about 0.4 seconds.
The force is related to the square of the ratio of those times. That's gives a measure of the low-down scale of tidal forces"
No.
The force that moves tides is not that simple. If it were, then lakes would go up and down in a similar range. They don't incidentally.
If you drop water in free fall, then it can fall because there is obviously nothing underneath it.
The sea is not in that position. For the surface to rise and fall, the water has to move sideways, or the water has to expand and contract.
The example you quoted of a tidal range of 2m in 6 hours is not a simple F=ma equation.
You have to bring in an incredibly complex range of factors including sea bottom shape, sea viscosity, flow patterns through constrictions, compressibility to name just the first ones off the top of my head.
Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
oggers,
The poor guy's written a decidedly mediocre conference proceeding that advances Mr Stokes' work from the 19th century not one jot....[etc etc blah blah yada yada]
The poor guy's written a decidedly mediocre conference proceeding that advances Mr Stokes' work from the 19th century not one jot....[etc etc blah blah yada yada]
25 posts since you first took issue with his work. 25 posts and not a single coherent argument that he has got anything wrong.
Where can I find your publishing history BTW?
Join Date: Dec 2007
Location: Pasadena
Posts: 633
Likes: 0
Received 0 Likes
on
0 Posts
Oggers, Laud his work if you want, that's your choice.
Tourist, deep large ocean tides are simple and do have that size - their driving force can be obtained to an order of magnitude from distance over time squared. Mr Newton did have it right. There is not enough water or extent in a lake to allow it to flow to respond like this in six hours via the necessary very-long-wavelength gravity waves.
Tourist, deep large ocean tides are simple and do have that size - their driving force can be obtained to an order of magnitude from distance over time squared. Mr Newton did have it right. There is not enough water or extent in a lake to allow it to flow to respond like this in six hours via the necessary very-long-wavelength gravity waves.
Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
Mr Optimistic
I can't help you with that. But while you're waiting, seeing as you wrote:
Please feel free to explain what he has got wrong. This is the Tech Log forum, so opinions require explanation, otherwise it defeats the purpose 
Oh dear do I have to repeat myself. I am asking for someone to explain this variable gravity theory of tides. If you can, fine, please do. If you can't I'll continue to wait.
Oh dear, he has stuffed up on his altitude dependent gravity.

Join Date: Dec 2007
Location: Pasadena
Posts: 633
Likes: 0
Received 0 Likes
on
0 Posts
What about the apparent change in gravity due to flying westwards/eastwards at 450kts?
Or are you worried about the relativistic corrections to timing, which are down at the 1 in 10-to-the-10 level, or the difference in co-rotation and counter-rotation terms in general relativity, which are stupendously small on scales of the Earth size and mass.
Join Date: Nov 2005
Location: Zulu Time Zone
Posts: 730
Likes: 0
Received 0 Likes
on
0 Posts
Oggers, Laud his work if you want, that's your choice.

And where can I find your publishing history BTW?



