1 in 60 rules and rate of descent, another technic? correct?
Thread Starter
Join Date: Jan 2020
Location: France
Posts: 30
Likes: 0
Received 0 Likes
on
0 Posts
1 in 60 rules and rate of descent, another technic? correct?
Hi I have a question regarding 060 Navigation module. I have used another technique than the prescribed 1 in 60 rule for this question, and I get a different result. I'd like to know if this technique
is at least correct.
Question: Given ILS glide path 3.5 degrees, GS = 150 kts. What is the ROD?
They use the 1 in 60 rule: (3.5x150x100)/ 60 = 875= approx 900 ft/min.
I did geometry: drawing a triangle of speeds, with :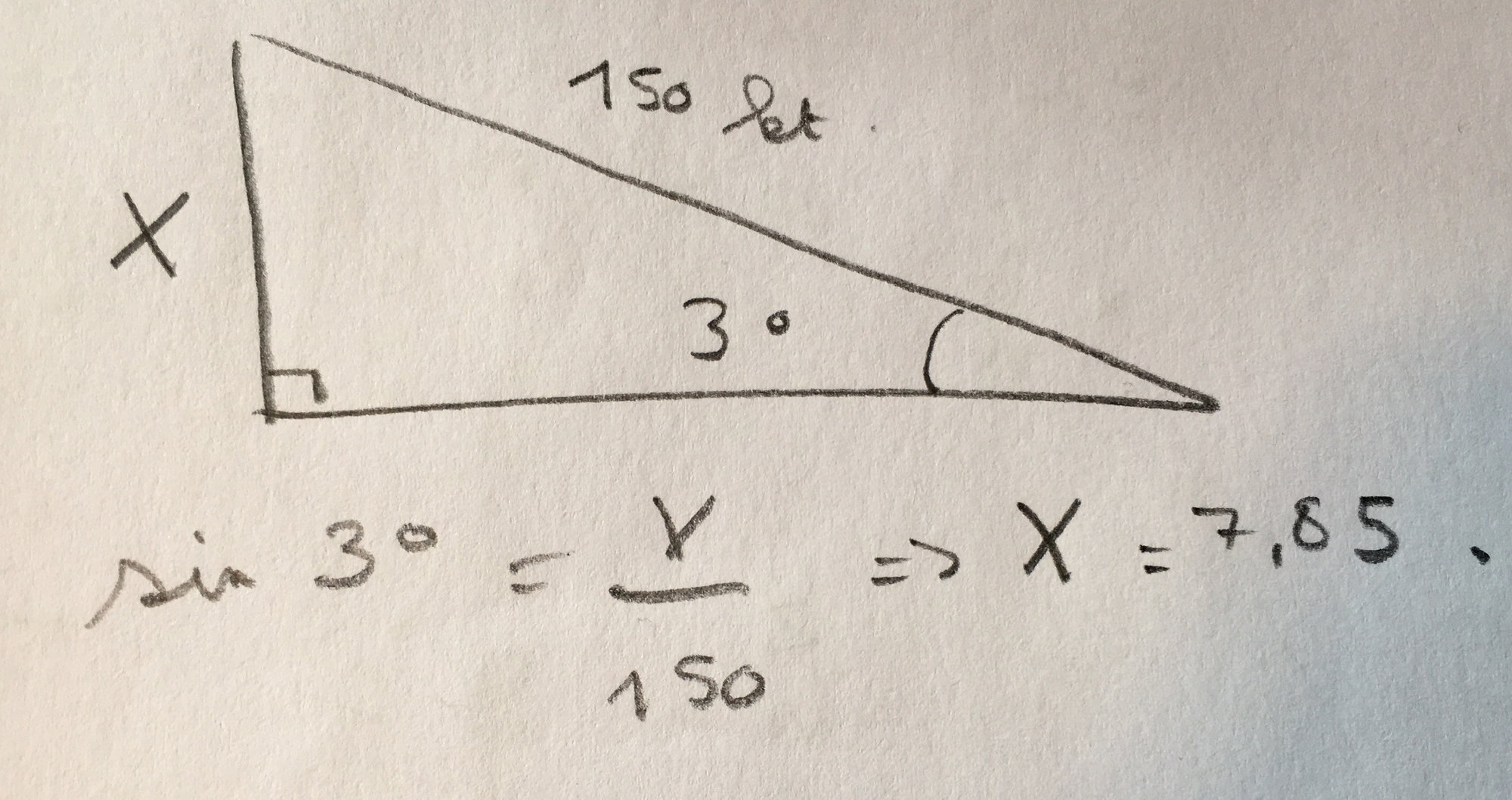
So the ROD is 7,85kts, which is 7,85NM/h, which is 7.85x6080 ft = 47728 ft/h which is (divided by 60min ) 795,47 ft/min close to 800 ft/min (NOT 900ft/min!)
is at least correct.
Question: Given ILS glide path 3.5 degrees, GS = 150 kts. What is the ROD?
They use the 1 in 60 rule: (3.5x150x100)/ 60 = 875= approx 900 ft/min.
I did geometry: drawing a triangle of speeds, with :
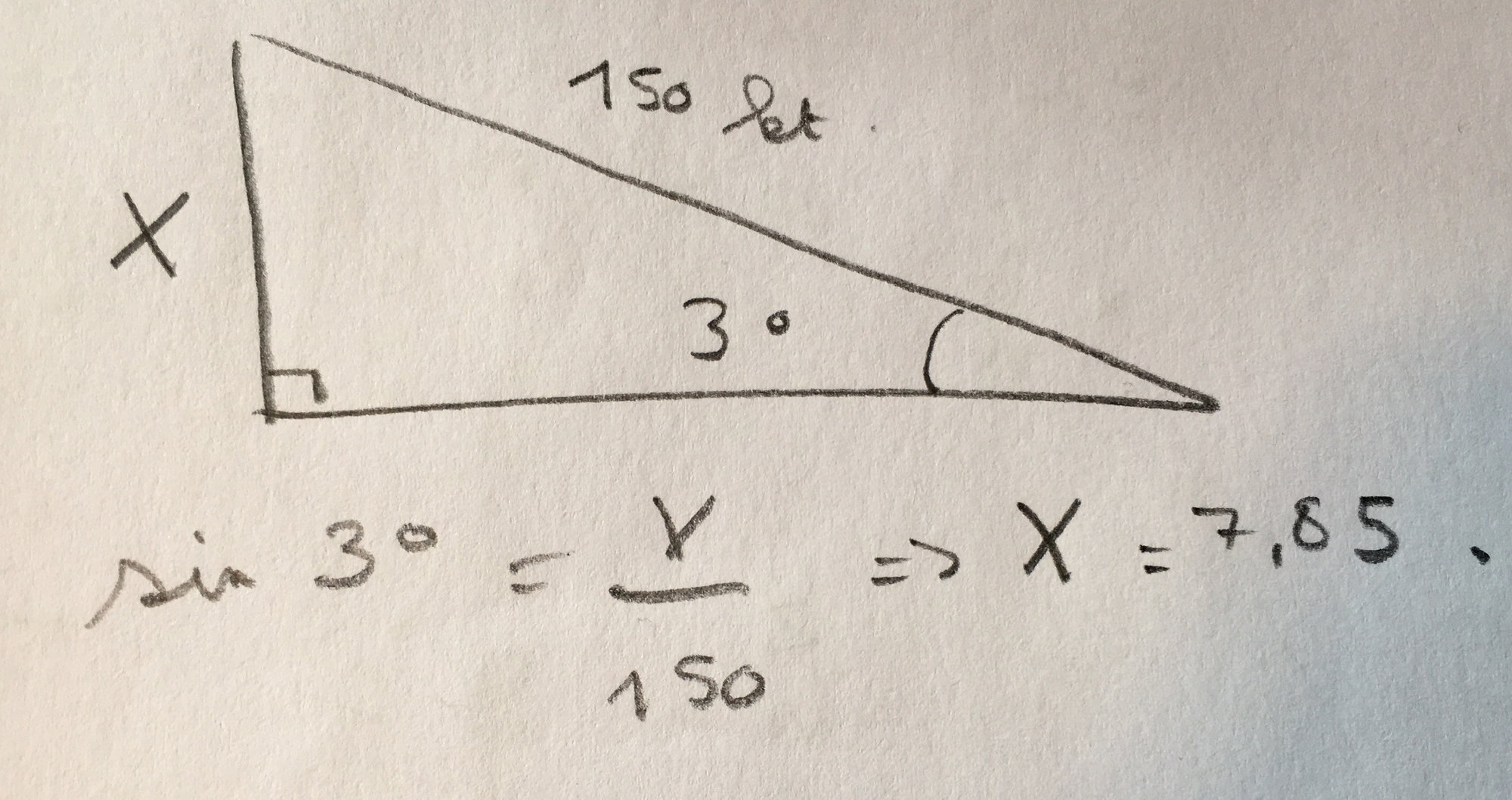
So the ROD is 7,85kts, which is 7,85NM/h, which is 7.85x6080 ft = 47728 ft/h which is (divided by 60min ) 795,47 ft/min close to 800 ft/min (NOT 900ft/min!)
Join Date: Dec 2000
Location: on the golf course (Covid permitting)
Posts: 2,131
Likes: 0
Received 0 Likes
on
0 Posts
At a VERY quick glance, in your first example you state a 3.5deg glideslope to get your answer.
In the second example you then use a 3 deg glideslope?
I'm obviously missing something
In the second example you then use a 3 deg glideslope?
I'm obviously missing something
Join Date: Dec 2015
Location: France
Posts: 507
Likes: 0
Received 0 Likes
on
0 Posts
Here is one technique, based on the "miles per minute".
For one nm per minute (60kt), the rate of descent corresponding to 1° is 100ft/min.
Example : at 150kt, you're at 2.5nm/min. So the rate of descent corresponding to 3.5° is 2.5*3.5*100 = 875ft/min
The exact figure is 927fpm, that is a 6% error.
This is useful because you can fly at multiples from 60kt.
eg, when in a descent at 420kt, one degree is 700ft/min (6% more in reality but who cares, the VS indicator does not differentiate between 700 and 742ft per min)
For one nm per minute (60kt), the rate of descent corresponding to 1° is 100ft/min.
Example : at 150kt, you're at 2.5nm/min. So the rate of descent corresponding to 3.5° is 2.5*3.5*100 = 875ft/min
The exact figure is 927fpm, that is a 6% error.
This is useful because you can fly at multiples from 60kt.
eg, when in a descent at 420kt, one degree is 700ft/min (6% more in reality but who cares, the VS indicator does not differentiate between 700 and 742ft per min)
Thread Starter
Join Date: Jan 2020
Location: France
Posts: 30
Likes: 0
Received 0 Likes
on
0 Posts
TopBunk
Your right thanks that solves it all!!
TheEdge
Oh God I annoy myself sometimes! thanks! This solves it all I do get 928 ft.min!! just because of that! so the triangle method IS right!! thank you!
Your right thanks that solves it all!!
TheEdge
Oh God I annoy myself sometimes! thanks! This solves it all I do get 928 ft.min!! just because of that! so the triangle method IS right!! thank you!
Thread Starter
Join Date: Jan 2020
Location: France
Posts: 30
Likes: 0
Received 0 Likes
on
0 Posts
Question solving, another technique 060 Navigation
Hi, I just wanted to show a technique i used which apparently is correct. It is for ATPL theory 060 navigation module.
The question states:
An aircraft T/O 2h before sunset, flying a track 090º(T), W/V 130º/20 kts, TAS 100kts. The correction he the admin used the computer, but i didn't. I found the GSo and GSh (Ground speed out and home), with cos(40º)=X/20, X the Head wind, X = 15kt. So Speed out is head wind so, GSo = 100-15 = 85 kts, and GSh back home is GSh = 100+15 = 115 kts. Now the only unvariable parameter is the time, we have 2 hours! And v=d/t (speed is distance over time), so t=d/v. In this case t = d/v1 +d/v2 indeed it is t= d/85+d/115, the time is both the same distance over the ground speed out PLUS + the same distance over the Ground speed home. then you can solve this equation:
t=2=(115d)/(9775)+(85d)/9775) finaly you get d = 97 NM!
The question states:
An aircraft T/O 2h before sunset, flying a track 090º(T), W/V 130º/20 kts, TAS 100kts. The correction he the admin used the computer, but i didn't. I found the GSo and GSh (Ground speed out and home), with cos(40º)=X/20, X the Head wind, X = 15kt. So Speed out is head wind so, GSo = 100-15 = 85 kts, and GSh back home is GSh = 100+15 = 115 kts. Now the only unvariable parameter is the time, we have 2 hours! And v=d/t (speed is distance over time), so t=d/v. In this case t = d/v1 +d/v2 indeed it is t= d/85+d/115, the time is both the same distance over the ground speed out PLUS + the same distance over the Ground speed home. then you can solve this equation:
t=2=(115d)/(9775)+(85d)/9775) finaly you get d = 97 NM!
Join Date: Oct 2007
Location: Wherever I go, there I am
Age: 43
Posts: 804
Likes: 0
Received 0 Likes
on
0 Posts
so the triangle method IS right
Join Date: May 2006
Location: UK
Posts: 105
Likes: 0
Received 0 Likes
on
0 Posts
You might need to be able to do the calculations in order to pass the exam, but when flying a real aeroplane, you won't be able to to the calculations in your head, before, or during an approach.
927 fpm isn't a practical parameter, so you might ask, other than being able to pass an exam, why are you required to be able to work it out ? ( about 1000/900/800/700 fpm depending on wind direction, it could be argued, are more practical numbers to learn ?
It's a bit like being able to plot a course with a pencil and a ruler on a chart. Had to do it in order to pass an ATPL exam many years ago, but never, ever, used the ability in practice.
It might be argued that the syllabus needs an overhaul ?
927 fpm isn't a practical parameter, so you might ask, other than being able to pass an exam, why are you required to be able to work it out ? ( about 1000/900/800/700 fpm depending on wind direction, it could be argued, are more practical numbers to learn ?
It's a bit like being able to plot a course with a pencil and a ruler on a chart. Had to do it in order to pass an ATPL exam many years ago, but never, ever, used the ability in practice.
It might be argued that the syllabus needs an overhaul ?
SID PLATE,
Yes, I saw that xplanefactor was talking about solving an exam question. Your point about exams vs practice is certainly valid.
What we did on the rare occasion when a rate of descent was needed for a non-precision approach (constant angle non-precision profile from FAF to MDA) was half the ground speed X10. And you could do this in your head. It gets you within +/-50fpm for a three degree descent path.
There's a reason they're called "non-precision" approaches.
Yes, I saw that xplanefactor was talking about solving an exam question. Your point about exams vs practice is certainly valid.
What we did on the rare occasion when a rate of descent was needed for a non-precision approach (constant angle non-precision profile from FAF to MDA) was half the ground speed X10. And you could do this in your head. It gets you within +/-50fpm for a three degree descent path.
There's a reason they're called "non-precision" approaches.

I think it is important to know how the values of flight parameters are calculated to give an understanding of what is going on. Hence exam questions like these.
Once that has all been understood and one is on the line in the cockpit though, rules of thumb are normally sufficient.
RoD for a 3° slope ~ 5 times the groundspeed, which as bafanguy mentioned, is much more easily worked out mentally as; Half the G/S, then add a zero.
It is important to have an idea of the approximate RoD expected; to guard against capturing false ILS glide-slopes and other gross errors.
Once that has all been understood and one is on the line in the cockpit though, rules of thumb are normally sufficient.
RoD for a 3° slope ~ 5 times the groundspeed, which as bafanguy mentioned, is much more easily worked out mentally as; Half the G/S, then add a zero.
It is important to have an idea of the approximate RoD expected; to guard against capturing false ILS glide-slopes and other gross errors.
The whole syllabus is based on these approximations, as it should be.




