Grandpa, what’s the farthest you can see?

[FullOppositeRudder]

This doesn't fit the properties of the discussion exactly, but last night we had an excellent overhead at dusk pass of the International Space Station which continued visually right down to the distant treeline on the south eastern horizon. Looking back at my tracking program for that pass, at that moment it was 2,150 km distant at an altitude of 434 km with a calculated elevation of about 2.5 degrees. Part of the fascination with this object is my involvement with the on-board amateur radio experiments, the rest is just the fascination of it being there, just as it was in October 1957 like watching the very first LEO object (Sputnik 1 launch vehicle) cross the sky. My grandmother was both skeptical and fearful - "Whatever next!" she said. None of us could have predicted what this would lead to in the years since that time and right up to our present era.

[visibility3miles]

I'm told that the sailors of old always knew that the hulls disappeared from view first, and the mast tops and crows nest's last, so they knew the earth was curved rather than flat when, for example, Christopher Columbus sailed away.

https://www.quora.com/What-is-the-di...-level?share=1

Originally Answered: How far is the horizon at sea level?As mentioned by others, the distance to the horizon at sea level (assuming you mean looking out over calm water) depends on what elevation you are viewing from. A good approximation for this when your observing height is relatively small compared to the radius of the Earth (in effect, not from the ISS!) is 𝑑=2𝑅ℎ‾‾‾‾√d=2Rh, where d is the distance to the horizon, R is the radius of the Earth, and h is the observation height.

As Chris Spencer wrote, this can be approximated as 𝑑=3.57ℎ‾‾√d=3.57h where h is in meters and d is in kilometers, or 𝑑=1.22ℎ‾‾√d=1.22h where h is in feet and d is in miles.

This would be great if we were on an airless planet, but in fact the distance to the horizon changes depending on the amount of atmospheric refraction, a function of temperature and pressure. In most cases, the atmosphere bends light rays downward, moving the horizon farther out. The equation is quite complicated and depends on knowing the atmospheric conditions quite precisely. However a reasonable approximation is either to increase the distance by 8%, or to replace the Earth’s radius by its effective radius, approximated to be 7/6 R. In which case the formulas become 𝑑=3.86ℎ‾‾√d=3.86h and 𝑑=1.32ℎ‾‾√d=1.32h.

Assuming an average overall height in the US, this would mean that the horizon IS 2.87 miles away, but appears to be 3.11 miles away.

[visibility3miles]

And, given my screen name, you know I was not supposed to fly if the visibility was less than three miles...

[kiwi grey]

From the car-park on Te Mata Peak (elevation ~400m, near Havelock North, Hawke's Bay, NZ), I have on an exceptionally clear day been able to see both Mt Ruapehu and Mt Taranaki.
Mt Taranaki is on the other side of the North Island and ~250km from Te Mata Peak

[MarianA]

Originally Posted by effortless

So his question is, how far from earth does an astronaut stop seeing more of the earth.

Supposing the astronaut is looking out the cupola of the ISS 400km above the surface of the earth I calculate a distance to the horizon of just under 2300km.



That means she sees the horizon 2300km from her vantage point.

The distance along the curvature on the ground an ant would have to travel will be slightly different. More different as your altitude above earth increases. Looking down from the moon almost the whole hemisphere will be visible and distance along the line of sight would be dominated by the distance from earth in the first place.

The math is just using the pythagorean theorem:



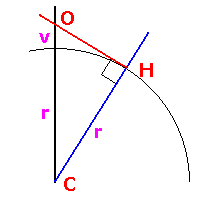
r=6400km
v=400km

The distance d from the Observer O to a point H on the horizon is given as the square root of

2*r*v+v^2

[goldox]

A few years ago one of the first 360 degree high-res photos of London was taken from (I think) the top of the Telecom Tower.
I remember scrolling and zooming around the image for ages being fascinated at what could be seen.
Looking due west I eventually zoomed as far as possible, and although quite hazy could clearly see tails of BA aircraft, airport buildings, and of course the tower.
I was mightily impressed.

[goldox]

Found it!
Height of viewing platform of BT Tower is 177 metres.
Distance to LHR tower is 20 miles.
Can't do any maths from this, not my thing....

[Midland 331]

A gin-clear December afternoon in Richmond, N.Yorks, U.K..

Aircraft seen con-trailing over Grimsby to the south-east, and Isle of Man to the west, all verified on FR24.

Heading up The East Coast to Teesside in the days of the "hang a left at Clacton" experimental rmilitary airspace routing, it was great to see the "bump" of Kent, then the tapering shape of The Wash, all weather map-style.

[GS-Alpha]

If you want the distance the ant travels (maintaining that the Earth is a sphere), you just need angle C. This can be calculated using the Sine rule:

OH/SinC = CO/SinH

SinH = Sin90 = 1

So SinC = OH/CO => AngleC = aSin(2298/6800) = 19.7515 degrees.

Distance the ant travels = Circumference of the Earth x 19.7515/360 = 2 x pi x 6400 x 19.7515/360 = 2206km.

(Something tells me the ant won’t survive the voyage).

[netstruggler]

As you move away from earth more and more of its hemisphere becomes visible.

But to see absolutely the whole hemisphere you'd need to be infinitely far away, such that the rays of light towards your eyes become parallel.

Luckily the universe allows for getting infinitely far away (perhaps).

[pilotmike]

For most applications, a simple approximation to within about 1%, which is close enough for most situations on Earth is:

D (Nautical Miles) = Square root of Height (Feet).

So to answer 'effortless's original question, the distance visible from 35,000' is around 190NM or 220 miles, not 700 miles. Apologies for making it appear so simple, when it can be made to sound so mathematically involved and over-complicated.

[scifi]

For those lucky enough to be really high above the earth, the amount of 'earth' that you can see is equal to 180 degrees minus the angle of the size of the earth.
So if earth subtends an angle of 30 degrees, you are actually seeing 180-30 , = 150 degrees of it.
Even when your earth only subtends an angle of 1 degree, you are still only seeing 179 degrees of it.
.

[Jan Olieslagers]

Grandpa, what’s the farthest you can see?

"Oh, that depends on many things, my big dear.
I've happened to not see your grandma just around the corner.
I've happened to see a B747 27 furlongs away."

With any luck, that will get him on about what a furlong is. Or a B747.

[treadigraph]

Had a lovely view of the ISS one night - noticed it was coming on the Portuguese coast around Porto so nipped up to my bedroom which faces SSE. Could see it clearly all the way across the Europe until it disappeared behind the flats opposite, probably near Warsaw or somewhere like that. In doing so it passed over the newly risen fullish moon and afterwards I could mentally trace its curved path from horizon to horizon - the earth is flat? Had another great view from Fort William - it was over Penzance when we spotted it!